MH's Blog
0%

CUDA实现FDTD算法的并行优化：针对空间划分

发表于 更新于 分类于

基于Development of a CUDA Implementation of the 3D FDTD Method

简单区域划分法

最显而易见的方法，区域划分法。将CUDA中的GRID与FDTD的网格相对应。

FDTD问题空间网格为：

CUDA的配置为：

对于一确定的Blcok(blockIdx.x, blockIdx.y, blockIdx.z)，其对应的FDTD网格范围（左闭右开）为：

其中$Q_x = \left \lceil \frac{N_x}{\text{Bs}_x} \right \rceil$，

其余方向同理。

由此得到一三元组，代表了一特定Blcok所负责计算的范围：

继续划分，可以容易得到一个线程所负责的计算范围：

其中$P_x = \left \lceil \frac{Q_x}{\text{Ts}_x} \right \rceil$，

其余方向同理。

简单易懂，但是需要正确配置。

对于一FDTD网格空间大小为$128 \times 128 \times 128$的问题，采用不同配置的CUDA配置。

  • $Bs = (128, 128, 2), Ts = (1, 1, 64)$: -g 128 128 2 -b 1 1 64 : 162.095 ms
  • $Bs = (128, 64, 4), Ts = (1, 2, 32)$: -g 128 64 4 -b 1 2 32 : 162.229 ms
  • $Bs = (128, 32, 8), Ts = (1, 4, 16)$: -g 128 32 8 -b 1 4 16 : 167.255 ms
  • $Bs = (128, 16, 16), Ts = (1, 8, 8)$: -g 128 16 16 -b 1 8 8 : 198.067 ms
  • $Bs = (64, 128, 2), Ts = (2, 1, 64)$: -g 64 128 2 -b 2 1 64 : 164.887 ms
  • $Bs = (64, 64, 4), Ts = (2, 2, 32)$: -g 64 64 4 -b 2 2 32 : 164.926 ms
  • $Bs = (64, 32, 8), Ts = (2, 4, 16)$: -g 64 32 8 -b 2 4 16 : 172.138 ms
  • $Bs = (64, 16, 16), Ts = (2, 8, 8)$: -g 64 16 16 -b 2 8 8 : 204.422 ms ms
  • $Bs = (32, 128, 2), Ts = (4, 1, 64)$: -g 32 128 2 -b 4 1 64 : 170.784 ms
  • $Bs = (32, 64, 4), Ts = (4, 2, 32)$: -g 32 64 4 -b 4 2 32 : 173.578 ms
  • $Bs = (32, 32, 8), Ts = (4, 4, 16)$: -g 32 32 8 -b 4 4 16 : 187.168 ms
  • $Bs = (32, 16, 16), Ts = (4, 8, 8)$: -g 32 16 16 -b 4 8 8 : 229.692 ms
  • $Bs = (16, 128, 2), Ts = (8, 1, 64)$: -g 16 128 2 -b 8 1 64 : 221.052 ms
  • $Bs = (16, 64, 4), Ts = (8, 2, 32)$: -g 16 64 4 -b 8 2 32 : 232.625 ms
  • $Bs = (16, 32, 8), Ts = (8, 4, 16)$: -g 16 32 8 -b 8 4 16 : 234.326 ms
  • $Bs = (16, 16, 16), Ts = (8, 8, 8)$: -g 16 16 16 -b 8 8 8 : 301.751 ms
  • $Bs = (2, 128, 128), Ts = (64, 1, 1)$: -g 2 128 128 -b 64 1 1 : 561.679 ms

先不分析，但显然这个方法对于如何配置CUDA是有一定要求的，正确配置可以得到较好的性能，而错误配置会导致性能下降。

简单区域划分法适配其他方法

4.2 Second Approach

文章Development of a CUDA Implementation of the 3D FDTD Method中的4.2 Second Approach中提到了一种划分方法，可以等价于简单区域划分法的一种特殊形式。

in this case, each thread executes all of the elements in the z direction in a for loop

考虑到C++行优先存储，应该等价于：

对于一FDTD网格空间大小为$128 \times 128 \times 128$的问题，采用不同配置的CUDA配置。

  • $Bs = (1, 128, 128), Ts = (1, 1, 1)$: -g 1 128 128 -b 1 1 1 : 2419.56 m
  • $Bs = (1, 64, 64), Ts = (1, 2, 2)$: -g 1 64 64 -b 1 2 2 : 838.7 ms
  • $Bs = (1, 32, 32), Ts = (1, 4, 4)$: -g 1 32 32 -b 1 4 4 : 372.919 ms
  • $Bs = (1, 16, 16), Ts = (1, 8, 8)$: -g 1 16 16 -b 1 8 8 : 328.063 ms
  • $Bs = (1, 8, 8), Ts = (1, 16, 16)$: -g 1 8 8 -b 1 16 16 : 228.957 ms
  • $Bs = (1, 4, 4), Ts = (1, 32, 32)$: -g 1 4 4 -b 1 32 32 : CUDA Error: too many resources requested for launch
  • $Bs = (1, 64, 64), Ts = (1, 1, 4)$: -g 1 64 64 -b 1 1 4 : 1383.64 ms
  • $Bs = (1, 32, 32), Ts = (1, 2, 8)$: -g 1 32 32 -b 1 2 8 : 524.478 ms
  • $Bs = (1, 16, 16), Ts = (1, 4, 16)$: -g 1 16 16 -b 1 4 16 : 385.855 ms
  • $Bs = (1, 16, 16), Ts = (1, 16, 4)$: -g 1 16 16 -b 1 16 4 : 387.436 ms
  • $Bs = (1, 8, 8), Ts = (1, 8, 32)$: -g 1 8 8 -b 1 8 32 : 309.327 ms
  • $Bs = (1, 8, 8), Ts = (1, 32, 8)$: -g 1 8 8 -b 1 32 8 : 286.032 ms

当然如果不考虑行优先存储，按照文章中的描述，应该是：

  • $Bs = (128, 128, 1), Ts = (1, 1, 1)$: -g 128 128 1 -b 1 1 1 : 1890.58 ms
  • $Bs = (64, 64, 1), Ts = (2, 2, 1)$: -g 64 64 1 -b 2 2 1 : 771.171 ms
  • $Bs = (32, 32, 1), Ts = (4, 4, 1)$: -g 32 32 1 -b 4 4 1 : 3259.66 ms
  • $Bs = (16, 16, 1), Ts = (8, 8, 1)$: -g 16 16 1 -b 8 8 1 : 3665.98 ms
  • $Bs = (8, 8, 1), Ts = (16, 16, 1)$: -g 8 8 1 -b 16 16 1 : 3743.38 ms
  • $Bs = (4, 4, 1), Ts = (32, 32, 1)$: -g 4 4 1 -b 32 32 1 : CUDA Error: too many resources requested for launch

显然，这种方法对于CUDA的启动配置也有一定要求。而且这种方法的性能没有达到最大化的并行度，正如文章所说：

Each approach has a maximum of xy NN × threads, where x N and y N are the size of the FDTD space in the x and y dimensions.

4.3 Third Approach

Block在二维上分配整个网格空间，Thread分配剩下的一维空间。

一种等价的分配形式为：

然而这并非是一个完美的等价，因为这种等价要求Thread只能在Z轴上分布，而文章的原意应该是允许Thread可以在任意方向上分布。当然要实现这么一个逻辑也很简单，但我想基于这个等价的性能测试也是足以说明问题的。

对于一FDTD网格空间大小为$128 \times 128 \times 128$的问题，采用不同配置的CUDA配置。

  • $Bs = (128, 128, 1), Ts = (1, 1, 64)$: -g 128 128 1 -b 1 1 64 : 179.11 ms
  • $Bs = (128, 128, 1), Ts = (1, 1, 32)$: -g 128 128 1 -b 1 1 32 : 287.759 ms
  • $Bs = (128, 128, 1), Ts = (1, 1, 16)$: -g 128 128 1 -b 1 1 16 : 331.508 ms
  • $Bs = (128, 128, 1), Ts = (1, 1, 8)$: -g 128 128 1 -b 1 1 8 : 551.388 ms

该方法锁死了配置，但是性能表现不错，基本上达到了最大并行度。
在CUDA中（至少在我的测试设备上），有如下参数：

Maximum number of thread per block: 1024
Maximum size of each dimension of a block: 1024 x 1024 x 64
Maximum size of each dimension of a grid: 2147483647 x 65535 x 65535

对于一般问题，该划分方法已经足够好了。基本上达到了越多线程越好的性能。

5. Our Implementations of the FDTD Method on GPU Hardware

相对于4.3方法提出了改进，提出了之前方法从未考虑到的问题Memory Access Pattern。

之前的方法对内存的访问模式是uncoalesced的，而这种访问模式会导致性能下降。

memory access is un-coalesced, since the threads within a block simultaneously access memory locations that are not adjacent.

为了实现coalesced memory access，即在同一个Block中的线程访问连续的内存，需要修正4.3中Thread的任务分配方式。不再使用threadRange作为任务分配方式。假定：

对任意一线程属于某个特定Block，其任务为：

是否存在一个更为普适的方法去表述这个任务分配方式呢？存在。

Decomposing Domain Based on Coalesced Memory Access

本质上不就是一维的获取吗？根本不需要这么麻烦。对问题空间：

实质上是一维数组存储的，只需要将其看作一维数组$[0, N_x \times N_y \times N_z)$，然后按照一维数组的方式去分配任务即可。

对于一确定的Block，其对应的FDTD网格范围（左闭右开）为：

对任意一线程属于某个特定Block，其任务为：

对于一FDTD网格空间大小为$128 \times 128 \times 128$的问题，采用不同配置的CUDA配置。

  • $Bs = (128, 128, 2), Ts = (1, 1, 64)$: -g 128 128 2 -b 1 1 64 : 159.378 ms
  • $Bs = (128, 64, 4), Ts = (1, 2, 32)$: -g 128 64 4 -b 1 2 32 : 157.845 ms
  • $Bs = (128, 32, 8), Ts = (1, 4, 16)$: -g 128 32 8 -b 1 4 16 : 157.851 ms
  • $Bs = (128, 16, 16), Ts = (1, 8, 8)$: -g 128 16 16 -b 1 8 8 : 157.825 ms
  • $Bs = (64, 128, 2), Ts = (2, 1, 64)$: -g 64 128 2 -b 2 1 64 : 157.839 ms
  • $Bs = (64, 64, 4), Ts = (2, 2, 32)$: -g 64 64 4 -b 2 2 32 : 157.679 ms
  • $Bs = (64, 32, 8), Ts = (2, 4, 16)$: -g 64 32 8 -b 2 4 16 : 157.768
  • $Bs = (64, 16, 16), Ts = (2, 8, 8)$: -g 64 16 16 -b 2 8 8 : 157.834 ms
  • $Bs = (32, 128, 2), Ts = (4, 1, 64)$: -g 32 128 2 -b 4 1 64 : 157.715 ms
  • $Bs = (32, 64, 4), Ts = (4, 2, 32)$: -g 32 64 4 -b 4 2 32 : 157.837 ms
  • $Bs = (32, 32, 8), Ts = (4, 4, 16)$: -g 32 32 8 -b 4 4 16 : 157.549 ms
  • $Bs = (32, 16, 16), Ts = (4, 8, 8)$: -g 32 16 16 -b 4 8 8 : 157.938 ms
  • $Bs = (16, 128, 2), Ts = (8, 1, 64)$: -g 16 128 2 -b 8 1 64 : 171.853 ms
  • $Bs = (16, 64, 4), Ts = (8, 2, 32)$: -g 16 64 4 -b 8 2 32 : 177.085 ms
  • $Bs = (16, 32, 8), Ts = (8, 4, 16)$: -g 16 32 8 -b 8 4 16 : 177.191 ms
  • $Bs = (16, 16, 16), Ts = (8, 8, 8)$: -g 16 16 16 -b 8 8 8 : 175.584 ms
  • $Bs = (2, 128, 128), Ts = (64, 1, 1)$: -g 2 128 128 -b 64 1 1 : 157.835 ms

比较简单区域划分法，这种方法不需要考虑如何配置CUDA，无论何种配置都可以得到几乎是最优的性能，中间有一段时间慢了20ms，可以发现是Block中包含了太多的线程，和资源有关TODO。

针对block大小的测试

  • $Bs = (256, 256, 2), Ts = (4, 4, 1)$: -g 256 256 2 -b 4 4 1 : 223.763 ms
  • $Bs = (256, 256, 1), Ts = (8, 4, 1)$: -g 256 256 1 -b 8 4 1 : 157.958 ms
  • $Bs = (256, 128, 1), Ts = (8, 8, 1)$: -g 256 128 1 -b 8 8 1 : 157.785 ms
  • $Bs = (128, 128, 1), Ts = (16, 8, 1)$: -g 128 128 1 -b 16 8 1 : 157.772 ms
  • $Bs = (128, 64, 1), Ts = (16, 16, 1)$: -g 128 64 1 -b 16 16 1 : 157.878 ms
  • $Bs = (128, 32, 1), Ts = (16, 32, 1)$: -g 128 32 1 -b 16 32 1 : 177.233 ms
  • $Bs = (64, 64, 1), Ts = (32, 16, 1)$: -g 64 64 1 -b 32 16 1 : 173.292 ms
  • $Bs = (32, 128, 1), Ts = (64, 8, 1)$: -g 32 128 1 -b 64 8 1 : 177.273 ms
  • $Bs = (64, 32, 1), Ts = (32, 32, 1)$: -g 64 32 1 -b 32 32 1 : CUDA Error: too many resources requested for launch

可以看到当Block中的Thread数量过多，大于等于512时, 会出现性能下降。当然也不能太小，一个Wrap中的Thread数量为32，所以最小也应该是32。

考虑和Second Approach的对比：

  • $Bs = (1, 128, 128), Ts = (1, 1, 1)$: -g 1 128 128 -b 1 1 1 : 2300.58 m
  • $Bs = (1, 64, 64), Ts = (1, 2, 2)$: -g 1 64 64 -b 1 2 2 : 753.165 ms
  • $Bs = (1, 32, 32), Ts = (1, 4, 4)$: -g 1 32 32 -b 1 4 4 : 289.601 ms
  • $Bs = (1, 16, 16), Ts = (1, 8, 8)$: -g 1 16 16 -b 1 8 8 : 200.878 ms
  • $Bs = (1, 8, 8), Ts = (1, 16, 16)$: -g 1 8 8 -b 1 16 16 : 214.539 ms
  • $Bs = (1, 4, 4), Ts = (1, 32, 32)$: -g 1 4 4 -b 1 32 32 : CUDA Error: too many resources requested for launch
  • $Bs = (1, 64, 64), Ts = (1, 1, 4)$: -g 1 64 64 -b 1 1 4 : 751.263 ms
  • $Bs = (1, 32, 32), Ts = (1, 2, 8)$: -g 1 32 32 -b 1 2 8 : 292.818 ms
  • $Bs = (1, 16, 16), Ts = (1, 4, 16)$: -g 1 16 16 -b 1 4 16 : 200.761 ms
  • $Bs = (1, 16, 16), Ts = (1, 16, 4)$: -g 1 16 16 -b 1 16 4 : 200.755 ms
  • $Bs = (1, 8, 8), Ts = (1, 8, 32)$: -g 1 8 8 -b 1 8 32 : 214.654 ms
  • $Bs = (1, 8, 8), Ts = (1, 32, 8)$: -g 1 8 8 -b 1 32 8 : 214.517 ms

全面的性能提升。

考虑和Third Approach的对比：

  • $Bs = (128, 128, 1), Ts = (1, 1, 64)$: -g 128 128 1 -b 1 1 64 : 166.745 ms
  • $Bs = (128, 128, 1), Ts = (1, 1, 32)$: -g 128 128 1 -b 1 1 32 : 175.438 ms
  • $Bs = (128, 128, 1), Ts = (1, 1, 16)$: -g 128 128 1 -b 1 1 16 : 231.391 ms
  • $Bs = (128, 128, 1), Ts = (1, 1, 8)$: -g 128 128 1 -b 1 1 8 : 432.519 ms

同样的全面的性能提升。

需要说明的是如果每一个Thread仅负责一个网格的计算，也就是总的网格数等于总的Thread数，那么Third Approach的内存访问模式就是coalesced的。

自动化

python脚本: pip install pyyaml

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
import os
import time
import yaml
import logging


class NcuMetric:
    def __init__(self, name, config):
        self.name = name
        self.ncu_path = config["ncu_path"]
        self.sections = config["sections"]
        self.rules = config["rules"]

    def to_command(self, output_file):
        cmd = f"{self.ncu_path}"
        for sec in self.sections:
            cmd += f" --section {sec}"
        for r in self.rules:
            cmd += f" --rule {r}"
        cmd += f" -f --export {output_file}"
        return cmd


class CudaLaunchConfig:
    def __init__(self, line):
        self.grid_dim = self._read_grid_dim(line)
        self.block_dim = self._read_block_dim(line)

    def _read_grid_dim(self, line):
        return line.split(" ")[1:4]

    def _read_block_dim(self, line):
        return line.split(" ")[5:8]

    def __str__(self):
        return f"-g {' '.join(self.grid_dim)} -b {' '.join(self.block_dim)}"

    def __repr__(self):
        return self.__str__()


class Case:
    def __init__(self, name, config):
        self.name = name
        self.cuda_launch_configs = self._make_cuda_launch_configs(config)

    def _make_cuda_launch_configs(self, config):
        return [CudaLaunchConfig(line) for line in config['args']]


class Exec:
    def __init__(self, name, config):
        self.name = name
        self.command = config["command"]
        self.work_dir = config["work_dir"]
        self.args = config["args"]

    def to_command(self):
        cmd = ''
        if not os.path.exists(self.command):
            err_str = f"Command {self.command} not found"
            raise FileNotFoundError(err_str)
        if not os.access(self.command, os.X_OK):
            raise PermissionError(err_str)
        cmd += self.command
        cmd += f" {self.args}"
        return cmd

class Group:
    def __init__(self, name, config):
        self.name = name
        self.output_dir = config["output_dir"]
        self.command_lines = config["command_lines"]


def make_file_name(e: Exec, c: Case, i: int, m: NcuMetric = None):
    grid_dim = c.cuda_launch_configs[i].grid_dim
    block_dim = c.cuda_launch_configs[i].block_dim
    prefix = f"{time.strftime("%Y_%m_%d", time.localtime())}_{e.name}_{c.name}_{
        i}_g_{'_'.join(grid_dim)}_b_{'_'.join(block_dim)}"
    if not m is None:
        prefix += f"_{m.name}"

    return prefix


def make_command_line(output_dir: str, e: Exec, c: Case, i: int, m: NcuMetric = None):
    cmd = e.to_command()
    name = make_file_name(e, c, i, m)
    cmd += f" {c.cuda_launch_configs[i]}"
    if not m is None:
        ncu_cmd = m.to_command(os.path.join(output_dir, name))
        cmd = f"{ncu_cmd} {cmd}"
    return cmd, name


def run(config):
    metrics = {}
    for metric in config["metrics"]:
        metrics[metric["name"]] = NcuMetric(metric["name"], metric)

    cases = {}
    for case in config["cases"]:
        cases[case["name"]] = Case(case["name"], case)

    execs = {}
    for e in config["execs"]:
        execs[e["name"]] = Exec(e["name"], e)

    groups = {}
    for group in config["groups"]:
        groups[group["name"]] = Group(group["name"], group)

    for g in groups.values():
        output_dir = g.output_dir
        if not os.path.exists(output_dir) and not os.path.isdir(output_dir):
            logging.warning(f"Output directory {
                            output_dir} not exists or not a directory. Create output directory")
            os.makedirs(output_dir)

        for item in g.command_lines:
            enable_profile = item["enable_profile"]
            e = execs[item["exec"]]
            c = cases[item["use_case"]]
            m = None
            cmd = ''
            if enable_profile:
                m = metrics[item["use_metric"]]

            for i in range(len(c.cuda_launch_configs)):
                try:
                    cmd, name = make_command_line(output_dir, e, c, i, m)
                    if not os.path.exists(e.work_dir):
                        logging.error(f"Command: {cmd} . Work directory {
                                      e.work_dir} not exists")
                        continue
                    if os.getcwd() != e.work_dir:
                        os.chdir(e.work_dir)

                    logging.info(f"Command: {cmd}")
                    err = os.system(f"{cmd} > {os.path.join(
                        output_dir, f'{name}.log')} 2>&1")
                    if err != 0:
                        err_str = f"Command {cmd} failed with error code {err}. "
                        err_str += f"Check log file {
                            os.path.join(output_dir, f'{name}.log')}"
                        raise Exception(err_str)
                except Exception as exception:
                    logging.error(exception)
                    continue


if __name__ == "__main__":
    logging.basicConfig(level=logging.INFO,
                        format="%(asctime)s - %(levelname)s - %(message)s")
    logging.info("Start benchmark")
    config_path = "config.yaml"
    with open(config_path, "r") as f:
        config = yaml.load(f, Loader=yaml.FullLoader)
    run(config)
    logging.info("End benchmark")

配置文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
metrics:
  - name: common
    ncu_path: /usr/local/NVIDIA-Nsight-Compute-2024.3/ncu
    sections:
      - LaunchStats
      - MemoryWorkloadAnalysis
      - MemoryWorkloadAnalysis_Chart
      - MemoryWorkloadAnalysis_Tables
      - Occupancy
      - SpeedOfLight
      - WarpStateStats
      - WorkloadDistribution
    rules:
      - AchievedOccupancy
      - CPIStall
      - Compute
      - LaunchConfiguration
      - Memory
      - MemoryApertureUsage
      - MemoryCacheAccessPattern
      - MemoryL2Compression
      - SOLBottleneck
      - SharedMemoryConflicts
      - TheoreticalOccupancy
      - ThreadDivergence
      - UncoalescedGlobalAccess
      - UncoalescedSharedAccess
      - WorkloadImbalance

cases:
  - name: one_to_one
    args:
      - -g 128 128 2 -b 1 1 64
      - -g 128 64 4 -b 1 2 32
      - -g 128 32 8 -b 1 4 16
      - -g 128 16 16 -b 1 8 8
      - -g 64 128 2 -b 2 1 64
      - -g 64 64 4 -b 2 2 32
      - -g 64 32 8 -b 2 4 16
      - -g 64 16 16 -b 2 8 8
      - -g 32 128 2 -b 4 1 64
      - -g 32 64 4 -b 4 2 32
      - -g 32 32 8 -b 4 4 16
      - -g 32 16 16 -b 4 8 8
      - -g 16 128 2 -b 8 1 64
      - -g 16 64 4 -b 8 2 32
      - -g 16 32 8 -b 8 4 16
      - -g 16 16 16 -b 8 8 8
      - -g 2 128 128 -b 64 1 1
  - name: second_approach
    args:
      - -g 1 128 128 -b 1 1 1
      - -g 1 64 64 -b 1 2 2
      - -g 1 32 32 -b 1 4 4
      - -g 1 16 16 -b 1 8 8
      - -g 1 8 8 -b 1 16 16
      - -g 1 4 4 -b 1 32 32
      - -g 1 64 64 -b 1 1 4
      - -g 1 32 32 -b 1 2 8
      - -g 1 16 16 -b 1 4 16
      - -g 1 16 16 -b 1 16 4
      - -g 1 8 8 -b 1 8 32
      - -g 1 8 8 -b 1 32 8
  - name: third_approach
    args:
      - -g 128 128 1 -b 1 1 64
      - -g 128 64 2 -b 1 2 32
      - -g 128 32 4 -b 1 4 16
      - -g 128 16 8 -b 1 8 8
  - name: coalesced_focus_block
    args:
      - -g 256 256 2 -b 4 4 1
      - -g 256 256 1 -b 8 4 1
      - -g 256 128 1 -b 8 8 1
      - -g 128 128 1 -b 16 8 1
      - -g 128 64 1 -b 16 16 1
      - -g 128 32 1 -b 16 32 1
      - -g 64 64 1 -b 32 16 1
      - -g 32 128 1 -b 64 8 1
      - -g 64 32 1 -b 32 32 1

execs:
  - name: uncoalesced
    command: /home/franzero/CPP/temp/XFDTD_CUDA/build/Release-x64/bin/benchmark
    work_dir: /home/franzero/CPP/temp/XFDTD_CUDA
    args: "-t 0 -s 3"
  - name: coalesced
    command: /home/franzero/CPP/XFDTD_CUDA/build/Release-x64/bin/benchmark
    work_dir: /home/franzero/CPP/XFDTD_CUDA
    args: "-t 0 -s 3"
  - name: uncoalesced_time
    command: /home/franzero/CPP/temp/XFDTD_CUDA/build/Release-x64/bin/benchmark
    work_dir: /home/franzero/CPP/temp/XFDTD_CUDA
    args: "-t 0 -s 100"
  - name: coalesced_time
    command: /home/franzero/CPP/XFDTD_CUDA/build/Release-x64/bin/benchmark
    work_dir: /home/franzero/CPP/XFDTD_CUDA
    args: "-t 0 -s 100"

groups:
  - name: ncu_profile
    output_dir: /home/franzero/XFDTD_CUDA_NCU_PROFILE
    command_lines:
      - enable_profile: true
        use_metric: common
        use_case: one_to_one
        exec: uncoalesced
      - enable_profile: true
        use_metric: common
        use_case: second_approach
        exec: uncoalesced
      - enable_profile: true
        use_metric: common
        use_case: third_approach
        exec: uncoalesced
      - enable_profile: true
        use_metric: common
        use_case: one_to_one
        exec: coalesced
      - enable_profile: true
        use_metric: common
        use_case: second_approach
        exec: coalesced
      - enable_profile: true
        use_metric: common
        use_case: third_approach
        exec: coalesced
      - enable_profile: true
        use_metric: common
        use_case: coalesced_focus_block
        exec: coalesced
  - name: running_time
    output_dir: /home/franzero/XFDTD_CUDA_RUNNING_TIME
    command_lines:
      - enable_profile: false
        use_case: one_to_one
        exec: uncoalesced_time
      - enable_profile: false
        use_case: second_approach
        exec: uncoalesced_time
      - enable_profile: false
        use_case: third_approach
        exec: uncoalesced_time
      - enable_profile: false
        use_case: one_to_one
        exec: coalesced_time
      - enable_profile: false
        use_case: second_approach
        exec: coalesced_time
      - enable_profile: false
        use_case: third_approach
        exec: coalesced_time
      - enable_profile: false
        use_case: coalesced_focus_block
        exec: coalesced_time

分析

1. 当每一个Thread仅负责一个网格的计算时

对uncoalesced memory access与coalesced memory access的性能对比。
取几个比较典型的配置进行对比。

  1. $Bs = (128, 128, 2), Ts = (1, 1, 64)$: -g 128 128 2 -b 1 1 64
  2. $Bs = (64, 64, 16), Ts = (2, 8, 8)$: -g 64 64 16 -b 2 8 8
  3. $Bs = (16, 16, 16), Ts = (8, 8, 8)$: -g 16 16 16 -b 8 8 8

对于uncoalesced memory access，所使用的时间分别为：162ms，204ms，301ms。
对于coalesced memory access，所使用的时间分别为：159ms，157ms，175ms。

uncoalesced memory access的性能比较。

基准线为：
128-128-2-base-gpu_u.png
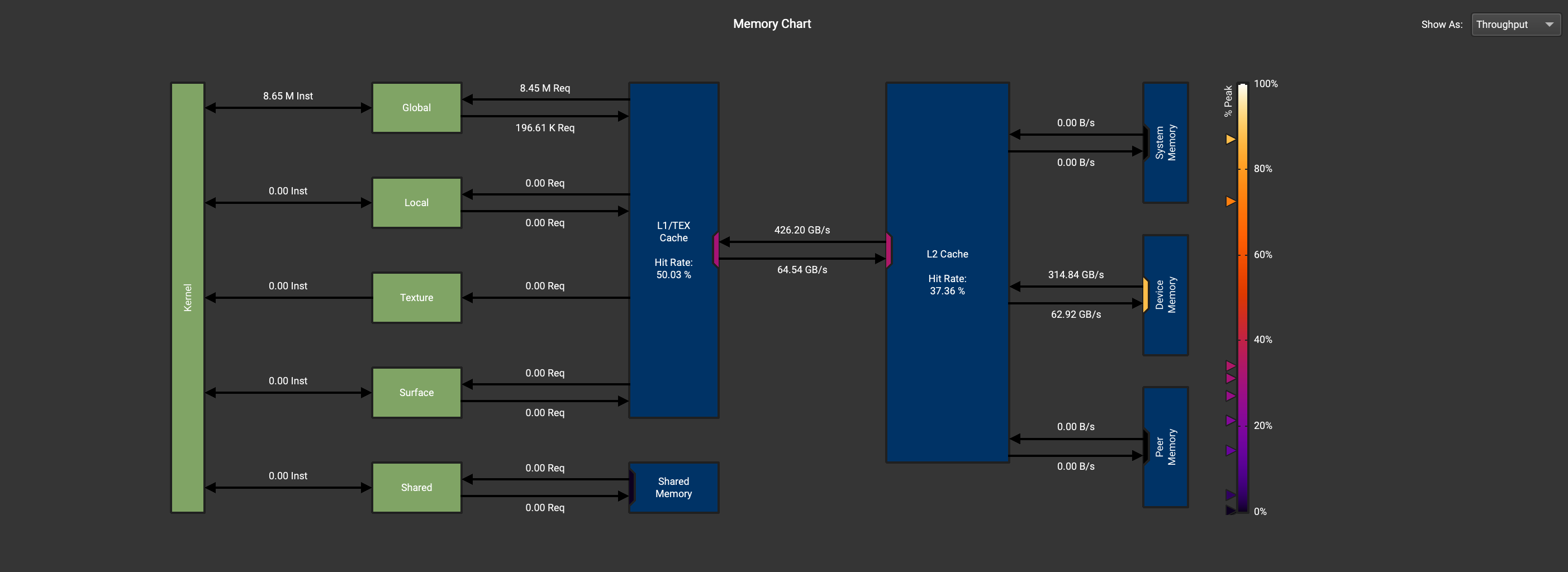
128-128-2-base-mem_u.png

对比64-64-16-2-8-8。

128-128-2-1-1-64-cmp-64-64-16.png

绿色为128-128-2-1-1-64，蓝色为64-64-16-2-8-8，可以发现绿色的MemoryThroughput的占比更大，ComputeThroughput的占比更小，
一般认为，FDTD算法的计算部分比较简单，限制FDTD性能的主要是内存带宽。

However, this explicitness also implies that making the next snapshot of the system requires the processing of all the electromagnetic field unknowns in the entire domain. Computationally, this means that all the unknowns must be moved between the RAM and the CPU at each time iteration. As all CPU cores on acomputing node share acommon addressable memory, this data movement creates abottleneck in shared-memory access. This isthe main performance-limiting factor, since ithinders making use of the CPU at full speed

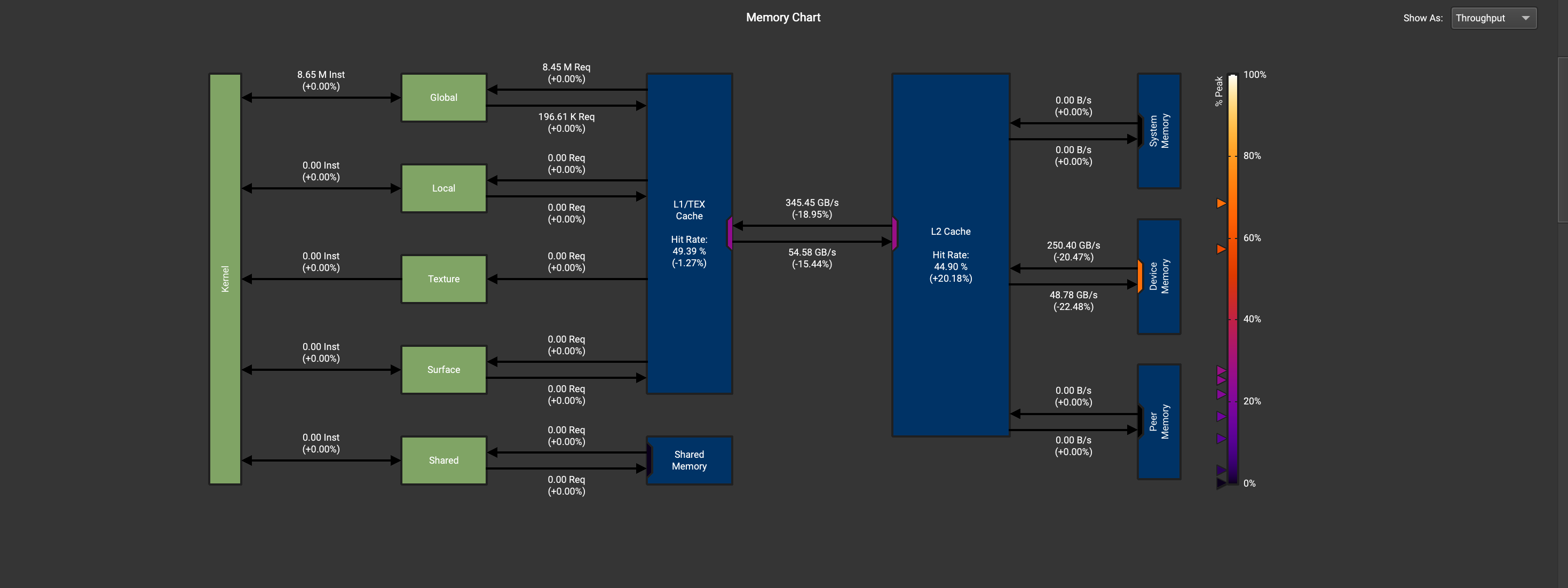
128-128-2-1-1-64-cmp-64-64-16-mem.png

数值为64-64-16-2-8-8比较的百分比为128-128-2-1-1-64，在内存吞吐量上，128-128-2-1-1-64比64-64-16-2-8-8高出了20%左右。

对比16-16-16-8-8-8，

128-128-2-cmp-16-16-16-gpu-u.png
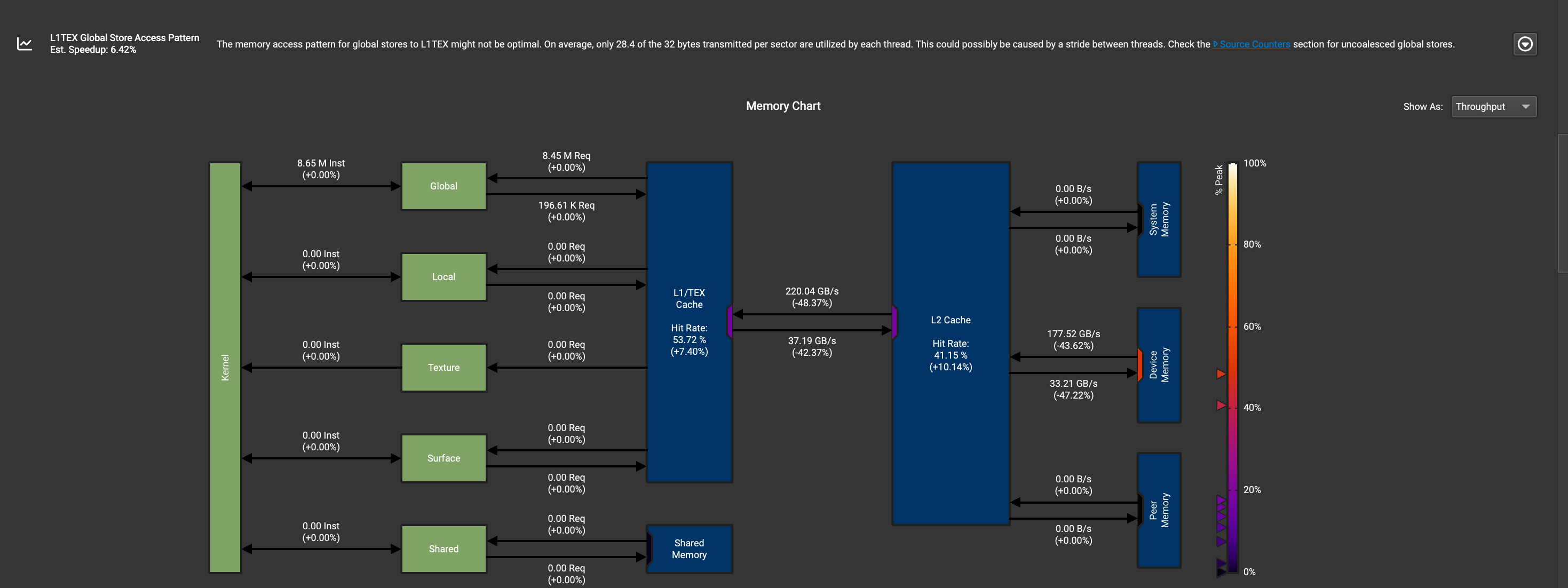
128-128-2-1-1-64-cmp-16-16-16-8-8-8-u.png

可以发现16-16-16-8-8-8所时间的时间更长，是因为内存吞吐量更低。

纵向比较，对比coalesced memory access的性能。

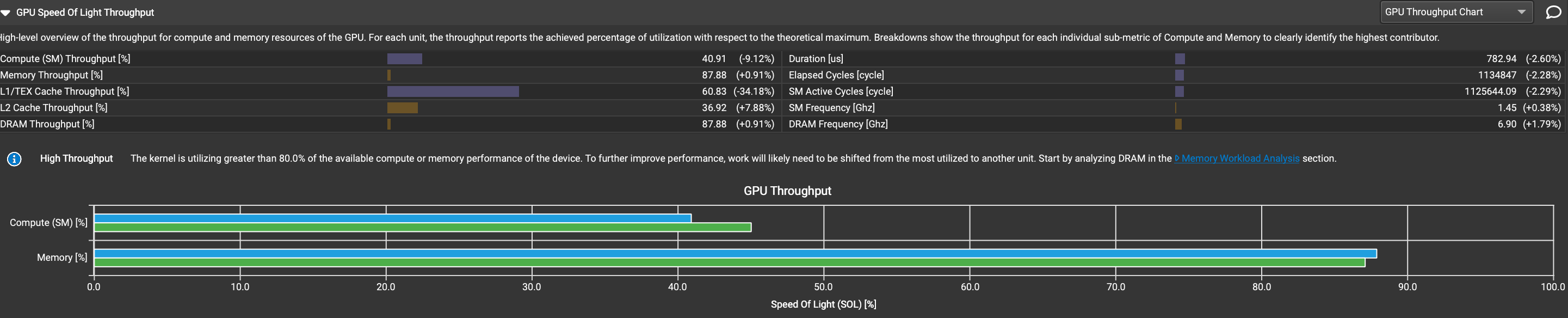
128-128-128-cmp-c-gpu.png
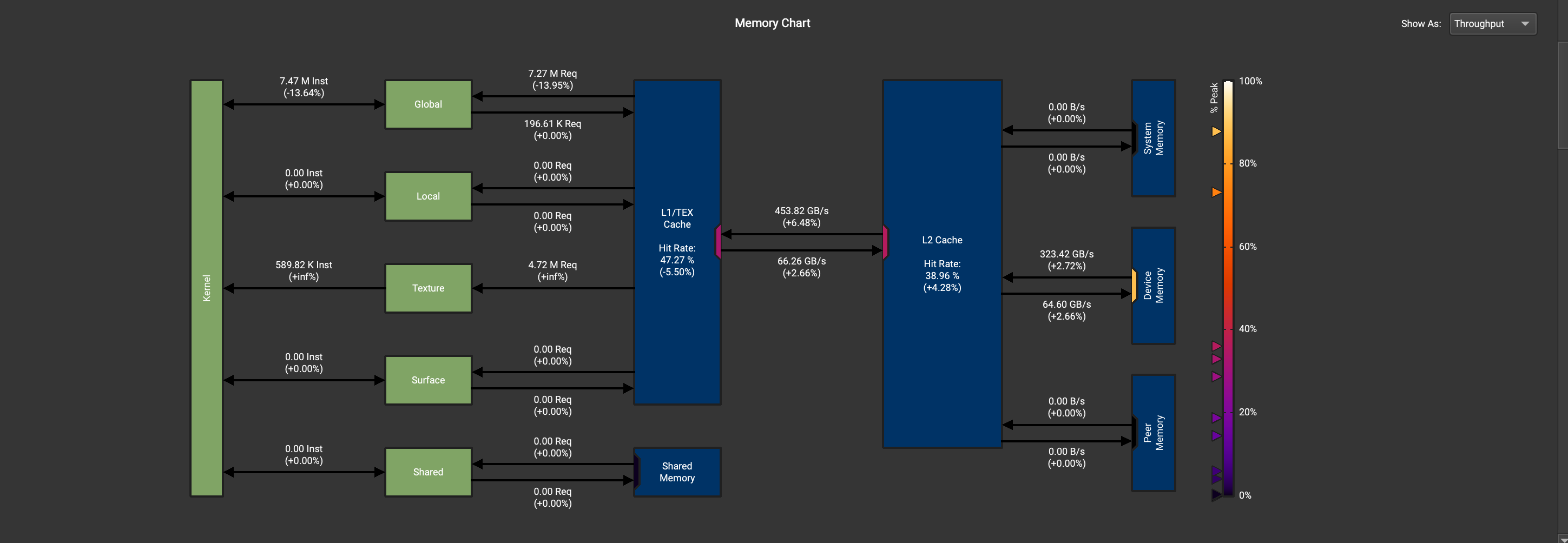
128-128-128-cmp-c-mem.png

吞吐量高了大约2%，所以时间上也只是差了一点点。