狭义相对论

基本原理

两条基本假设：

1. 相对性原理：所有惯性参考系都是等价的。物理规律对于所有惯性参考系都可以表为相同形式。
2. 光速不变原理：真空中的光速相对于任何惯性系沿任一方向恒为c，并与光源运动无关。

在经典物理学与狭义相对论中，惯性参考系或惯性坐标系，简称为惯性系（英语：Inertial frame of reference）是指可以均匀且各向同性地描述空间，并且可以均匀描述时间的参考系。在这个前提下，两个惯性系中的时空变换只能是线性变换。

$$\begin{equation} \begin{bmatrix} x^{'}\\ y^{'}\\ z^{'}\\ ct^{'}\\ \end{bmatrix} = A \begin{bmatrix} x\\ y\\ z\\ ct\\ \end{bmatrix} \end{equation}$$

假设$\bar{S}$相对于$S$的速度为$v$，且仅在$x$轴上运动，令$t=\bar{t}=0$时刻，两参考系坐标原点重合。

间隔不变性

物质运动可以看作一连申事件的发展过程，事件总是在一定地点于一定时刻发生的，可令$(x,y,z,t)$代表一事件（一个事件对应唯一一个时空点，但一个时空点可以对应多个事件）。考虑事件1：在原点时发出一道光。事件2：在P点接收到这一道光。

对于参考系$S$，事件1为$(0,0,0,0)$，事件2为$(x,y,z,t)$。
对于参考系$\bar{S}$，事件1为$(0,0,0,0)$，事件2为$(\bar{x},\bar{y},\bar{z},\bar{t} )$。
由于光速不变原理。

$$\begin{equation} \begin{aligned} x^2+y^2+z^2 = c^2t^2\\ \bar{x}^2+\bar{y}^2+\bar{z}^2 = c^2 \bar{t}^2\\ \end{aligned} \end{equation}$$

上面我们选择了两特殊事件，这两事件之间用光讯号联系着. 一般来说，两事件不一定用光讯号联系，它们可能用其他方式联系，或者根本没有任何联系。在一般情况下，我们有：

$$\begin{equation} \begin{aligned} x^2+y^2+z^2 - c^2t^2 = a \\ \bar{x}^2+\bar{y}^2+\bar{z}^2 - c^2 \bar{t}^2 = b \\ \end{aligned} \end{equation}$$

由于两参考系的时空变换是线性的，我们可以找到一线性变换$F$使得两式相等（为什么呢），又当$a=0$时，有$b=0$，所以这个线性变换只能是乘上一常数因子$B$，即为：

$$\begin{equation} x^2+y^2+z^2 - c^2t^2 = B (\bar{x}^2+\bar{y}^2+\bar{z}^2 - c^2 \bar{t}^2) \end{equation}$$

这个常数因子只可能依赖于两参考系相对速度的绝对值（因为在空间中不存在特定方向），因为两参考系是等价的反之也有$S$变换到$\bar{S}$时也乘上$B$即可，所以$B^2=1$，由变换的连续性可知（自己变自己不变），$B=1$。

所以有：

$$\begin{equation} -s^2 = x^2+y^2+z^2 - c^2t^2 = \bar{x}^2+\bar{y}^2+\bar{z}^2 - c^2 \bar{t}^2 = -\bar{s}^2 \end{equation}$$

这就是光速不变性的数学表示，其中$s^2$称作事件的间隔，这也是间隔不变性，它表示两事件的间隔不因参考系变换而改变。一般而言，间隔表示为：

$$\begin{equation} s^2 = c^2 (t_2^2 - t_1^1)^2 - (x_2^2 - x_1^1)^2 - (y_2^2 - y_1^1)^2 - (z_2^2 - z_1^1)^2 \end{equation}$$

洛伦兹变换

$$\begin{equation} A = \begin{bmatrix} \gamma & 0 & 0 & -\beta\gamma \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ -\beta\gamma & 0 & 0 & \gamma \\ \end{bmatrix} \end{equation}$$

其中：

$$\begin{equation} \gamma = \frac{1}{\sqrt{1 - \beta^2}}, \quad \beta = \frac{v}{c} \end{equation}$$

时空理论

两事件的间隔可以取任何数值.我们区别三种情况：

1. 若两事件可以用光波联系，则$s^2 = 0$
2. 若两件事可以用速度低于光速的作用联系，则$s^2 > 0$
3. 若两事件的空间距离超过光波的作用速度，则$s^2 < 0$

这里我用一个二维图表示。

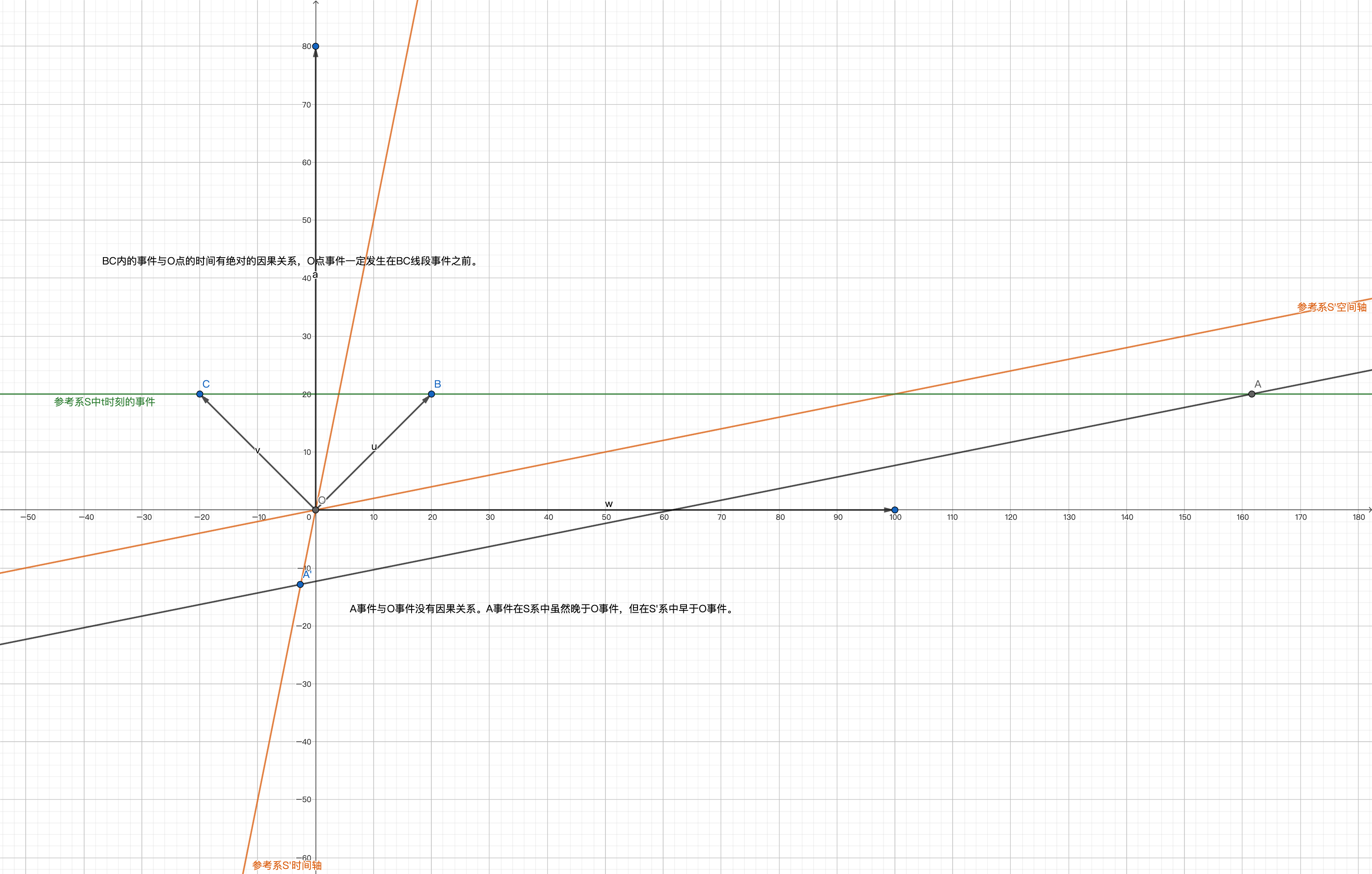
1. 称作类光间隔
2. 称作类时间隔
   • 绝对未来
   • 绝对过去
3. 称作类空间隔

类时间隔和类空间隔时截然不同的两种时空关系。

因果律

事物发展有一定因果关系，通过物质运动的联系，作为原因的第一事件导致作为结果的第二事件，这种因果关系时绝对的。

在类时间隔中，如果不存在超光速的互相作用，事件的发生有必然先后次序，不与参考系的选取有关，因而有绝对的因果关系。

相对论时空观完全符合因果律的要求。

同时的相对性

类空间隔，有不存在超光速作用，所以两件事绝对没有因果关系，两件事的发生也就没有先后次序之分。

在不同地点同时发生的两事件不可能有因果关系，因此同时概念必然是相对的，是相对于参考系而言的。

时钟延缓

相对$S$系中体静止的某物体内部发生一物理过程（比如分子振动的一个周期），其事件1为$(x,t_1)$事件2为$(x,t_2)$，则时间$\Delta \tau = t_2 - t_1$，在$\bar{S}$系中两件事的时间间隔$\Delta t = \gamma \Delta \tau$。（这个可以用洛伦兹变换得出，或者间隔不变性）。

尺度收缩

相对于$\bar{S}$系静止的物体，长度为$L_0$，在$S$系中同时量取两端长度$L$有：

$$\begin{equation} s^2 = -(x_2 - x_1)^2 = -L^2 = c^2(\bar{t_2} - \bar{t_1})^2 - (\bar{x_2} - \bar{x_1})^2 = c^2(\bar{t_2} - \bar{t_1})^2 - L_0^2 \end{equation}$$

得：

$$\begin{equation} L = \frac{L_0}{\gamma} \end{equation}$$

动尺的缩短是同时的相对性的直接后果。

速度变换

在参考系$S$中，速度为：

$$\begin{equation} \vec{u} = \frac{\mathrm{d}\vec{r}}{\mathrm{d}t} = i\frac{\mathrm{d}x}{\mathrm{d}t} + j\frac{\mathrm{d}y}{\mathrm{d}t} + k\frac{\mathrm{d}z}{\mathrm{d}t} \end{equation}$$

在参考系$\bar{S}$中，有：

$$\begin{equation} \mathrm{d} \begin{bmatrix} \bar{x}\\ \bar{y}\\ \bar{z}\\ c\bar{t}\\ \end{bmatrix} = A \mathrm{d} \begin{bmatrix} x\\ y\\ z\\ ct\\ \end{bmatrix} \end{equation}$$

运动介质中的光速。

一介质相对于$\bar{S}$静止，其折射率为$n$。

在$\bar{S}$系中，光在介质中沿着$+x$方向的传播速度为：

$$\begin{equation} \bar{u} = \frac{c}{n} = \frac{\mathrm{d}\bar{x}}{\mathrm{d}\bar{t}} \end{equation}$$

则在$S$系中：

$$\begin{equation} u = \frac{\mathrm{d}x}{\mathrm{d}t} = \frac{v + \frac{c}{n}}{1 + \frac{v}{nc}} \end{equation}$$

变换一下：

$$\begin{equation} u = u - \frac{c}{n} + \frac{c}{n} = \frac{v(1 - \frac{1}{n^2})}{1 + \frac{v}{nc}} + \frac{c}{n} \end{equation}$$

若$v$远小于$c$。

$$\begin{equation} u = \frac{c}{n} + (1 - \frac{1}{n^2})v \end{equation}$$

相对论理论的四维形式

亨利·庞加莱在1905年至1906年间发现当将时间作为一个虚坐标ict（其中c为光速，i是虚数单位）并与三个表示空间的实坐标共同组成四维时空时，洛伦兹变换就可以看作是这一时空中的坐标旋转。

赫尔曼·闵可夫斯基基于这一构想在四维空间中重新阐释了麦克斯韦方程组，并展示了其在洛伦兹变换前后的不变性。[5]他又进一步在四维空间中重新表述了爱因斯坦的狭义相对论，由此总结出时间与空间应该做相同的处理，并提出了事件是在一个统一的四维时空连续统中发生的概念。

物理量的分类

三维空间中，空间的转动就是一个正交变换。

$$\begin{equation} \bar{x}_i = \sum_{j=1}^{3}{a_{ij}x_j} \end{equation}$$

简记为

$$\begin{equation} \bar{x}_i = a_{ij}x_j \end{equation}$$

当出现重复下标时意味着求和。

标量：空间转动后不变的量。$\bar{u}=u$

矢量：转动后的变换关系为：

$$\begin{equation} \bar{v}_i = a_{ij}v_j \end{equation}$$

张量：如二阶张量：

$$\begin{equation} \bar{T}_{ij} = a_{ik}a_{jl} T_{kl} \end{equation}$$

洛伦兹变换满足间隔不变性。如果令：

$$\begin{equation} x_4 = \mathrm{i}ct \end{equation}$$

有：

$$\begin{equation} x_{\mu}x_{\mu} = \bar{x}_{\mu}\bar{x}_{\mu} \end{equation}$$

洛伦兹变换形式上可以看作四维空间的转动，这四维空间的第四个坐标是虚数，因此它是复四维空间，不同于实数的四维欧几里得空间。线性变换为：

$$\begin{equation} A = \begin{bmatrix} \gamma & 0 & 0 & \mathrm{i}\beta\gamma \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ -\mathrm{i}\beta\gamma & 0 & 0 & \gamma \\ \end{bmatrix} \end{equation}$$

See more: https://en.wikipedia.org/wiki/Minkowski_space

四维协变量

把三维情形推广，我们也可以按照物理量在四维空间转动下的变换性质来把物理量分类。在洛伦兹变换下不变的物理量称为洛伦兹标量或不变量。

四维矢量：

$$\begin{equation} \bar{V}_{\mu} = a_{\mu \nu}V_{\nu} \end{equation}$$

四维张量：

$$\begin{equation} \bar{T}_{\mu \nu} = a_{\mu \lambda}a_{\nu \tau}T_{\lambda \tau} \end{equation}$$

这些物理量（标量、矢量和各阶张量）在洛伦兹变换下有确定的变换性质，称为协变量。

如间隔：$ds^2 = -dx{\mu}dx{\mu}$为洛伦兹标量。固有时也是一个洛伦兹标量$d \tau = \frac{1}{c \cdot ds}$。

定义：

$$\begin{equation} U_{\mu} = \frac{\mathrm{d}x_{\mu}}{\mathrm{d} \tau} \end{equation}$$

称为四维速度矢量。

通常我们定义速度为：

$$\begin{equation} u_{i} = \frac{\mathrm{d} x_i}{\mathrm{d} t} \end{equation}$$

注意这两个的区别，对于$u_{i}$我们之前已经得到速度变换式。

由时间延缓效应：

$$\begin{equation} \frac{\mathrm{d}t}{\mathrm{d}\tau} = \gamma \end{equation}$$

我们有：

$$\begin{equation} U_{\mu} = \gamma (u_1, u_2, u_3, ic)^T \end{equation}$$

TODO

1. 固有时的概念
2. https://en.wikipedia.org/wiki/Lorentz_transformation#Proper_transformations