一维FDTD计算编程实例

考虑真空中，一无限大平面电流源：

$$\vec{J}(z, t) = - \hat{x} I \cdot \cos(\omega t + \phi) \cdot \delta(z)$$

其中$\delta(z)$为冲激函数。求解电磁场分布。

解析式

使用Fourier变换将时域转为频域：

$$\vec{J}(z, t) = - \Re\left[ I \delta(z) \exp(\jmath \omega t + \phi) \right] \cdot \hat{x}\tag {1-2}$$

其中$F(\omega)$是$\cos(\omega t + \phi)$的傅里叶变换对。

对无源区，有时谐电磁场波动方程：详见FDTD前期准备

$$\begin{cases} \nabla^2 \vec{E} + k \frac{\partial^2 \vec{E}}{\partial t^2} & = 0 \\ \nabla^2 \vec{H} + k \frac{\partial^2 \vec{H}}{\partial t^2} & = 0 \\ k = \frac{\omega^2}{\epsilon \mu} \end{cases} \tag {1-3}$$

可解得：

$$\begin{cases} \vec{E}(z, \omega) & = \vec{E}^+(z) \exp(-\jmath kz) + \vec{E}^-(z) \exp(\jmath kz) \\ \vec{H}(z, \omega) & = \vec{H}^+(z) \exp(-\jmath kz) + \vec{H}^-(z) \exp(\jmath kz) \\ \end{cases} \tag {1-3}$$

$\vec{E}^+(z) \exp(-\jmath kz)$是沿z轴正方向传播，反之反之。

由对称性不难得出：

$$\begin{cases} \vec{H}(z, \omega) & = \hat{y} H^+(z) \exp(-\jmath kz) & z > 0 \\ \vec{H}(z, \omega) & = \hat{y} H^-(z) \exp(\jmath kz) & z < 0 \\ \end{cases}$$

由Maxwell方程中的：$\nabla \times \vec{H} - \frac{\partial \vec{D}}{\partial t} = \vec{J}$，取一边长为a的正方形yoz面。可得：

$$2 a |H_y| = a I \Rightarrow |H_y| = \frac{I}{2} \tag {1-1}$$

以后填坑，实在没明白时域频域互转。

解析解：

$$\begin{cases} \vec{H}(z, t) & = \hat{y} \frac{I}{2} \cos(\omega t - kz + \phi) & z > 0 \\ \vec{H}(z, t) & = \hat{y} \frac{I}{2} \cos(\omega t + kz + \phi) & z < 0 \\ \vec{E}(z, t) & = \hat{x} \frac{I}{2Z_0} \cos(\omega t - kz + \phi) & z > 0 \\ \vec{E}(z, t) & = -\hat{x} \frac{I}{2Z_0} \cos(\omega t + kz + \phi) & z < 0 \\ \end{cases}$$

FDTD计算

在$z = 0$和$z = 500 \Delta t$边界采用一阶Mur近似吸收边界，区域中心为平面电流源

获取差分公式

对于该问题，真空中一维FTDT问题，为求解TEM波。则对于麦克斯韦旋度方程有：

$$\begin{cases} - \frac{\partial H_y}{\partial z} = \epsilon_0 \frac{\partial E_x}{\partial t} + \sigma E_x \\ \frac{\partial E_x}{\partial z} = - \mu_0 \frac{\partial H_y}{\partial t} -\sigma_m H_y \\ \end{cases}$$

元胞不含电流源

元胞不含电流源，且真空中无损耗，有：

$$\begin{cases} - \frac{\partial H_y}{\partial z} = \epsilon_0 \frac{\partial E_x}{\partial t} \\ \frac{\partial E_x}{\partial z} = - \mu_0 \frac{\partial H_y}{\partial t} \\ \end{cases}$$

差分有：

$$\begin{aligned} - \frac{H_y^{n+1/2}(k + 1/2) - H_y^{n+1/2}(k-1/2)}{\Delta z} = \epsilon_0 \frac{E_x^{n+1}(k) - E_x^n(k)}{\Delta t} \\ E_x^{n+1}(k) = E_x^n(k) - \frac{\Delta t}{\epsilon_0} \frac{H_y^{n+1/2}(k + 1/2) - H_y^{n+1/2}(k-1/2)}{\Delta z} \\ E_x^{n+1}(k) = CA \cdot E_x^n(k) - CB \cdot [H_y^{n+1/2}(k + 1/2) - H_y^{n+1/2}(k-1/2)] \end{aligned}$$

对应Fortran代码：

Ex(z,t) = ca * Ex(z, t - 1) - cb * ( Hy(z, t - 1) - Hy(z - 1, t - 1) )

求Hy也同理有：

$$\begin{aligned} \frac{E_x^{n}(k+1) - E_x^{n}(k)}{\Delta z} = \mu_0 \frac{H_y^{n+1/2}(k+1/2) - H_y^{n-1/2}(k+1/2)}{\Delta t} \\ H_y^{n+1/2}(k+1/2) = H_y^{n-1/2}(k+1/2) + \frac{\Delta t}{\mu_0} \frac{E_x^{n}(k+1) - E_x^{n}(k)}{\Delta z} \\ H_y^{n+1/2}(k+1/2) = CP \cdot H_y^{n-1/2}(k+1/2) - CQ \cdot [E_x^{n}(k+1) - E_x^{n}(k)] \end{aligned}$$

对应Fortran代码：

Hy(z,t) = cp * Hy(z, t - 1) - cq * ( Ex(z + 1, t) - Ex(z, t) )

元胞包含电流源

假定在$z=k_s$处包含，且电流源附近是无耗介质。因为该电流源不是磁电流源，则只需改变$- \frac{\partial H_y}{\partial z} = \epsilon_0 \frac{\partial E_x}{\partial t}$

原始的微分形式为：

$$- \frac{\partial H_y}{\partial z} = \epsilon_0 \frac{\partial E_x}{\partial t} + \sigma E_x$$

这里把右边最后一项拆解为：

$$\sigma E_x = J_x + \sigma E_x$$

即一是：外部强加电流，二是：服从欧姆定律的传导电流。

电流源附近是无耗介质，则：

$$- \frac{\partial H_y}{\partial z} = \epsilon_0 \frac{\partial E_x}{\partial t} + J_x$$

对于该问题而言，面电流密度：

$$J_x = \frac{I \cdot \cos(\omega t + \phi)}{\Delta z}$$

代入有：

$$\begin{aligned} E_x^{n+1}(k_s) = E_x^n(k_s) - \frac{\Delta t}{\epsilon_0} \frac{H_y^{n+1/2}(k_s + 1/2) - H_y^{n+1/2}(k_s-1/2)}{\Delta z} - \frac{\Delta t}{\epsilon_0} \frac{I(n+1/2)}{\Delta z} \\ E_x^{n+1}(k) = CA \cdot E_x^n(k) - CB \cdot [H_y^{n+1/2}(k + 1/2) - H_y^{n+1/2}(k-1/2)] - CB \cdot \frac{I(n+1/2)}{\Delta z} \end{aligned}$$

对应Fortran代码：

Ex(z,t) = ca * Ex(z, t - 1) - cb * ( Hy(z, t - 1) - Hy(z - 1, t - 1) ) - cb * current_source( (t + 0.5) * delta_t )

截断边界

一维Mur吸收边界的解析式：

$$\begin{cases} \left. \left( \frac{\partial f}{\partial z} - \frac{1}{v} \frac{\partial f}{\partial t} \right) \right |_{z = 0} = 0 \\ \left. \left( \frac{\partial f}{\partial z} + \frac{1}{v} \frac{\partial f}{\partial t} \right) \right |_{z = z_0} = 0 \\ \end{cases}$$

左边界：

要计算的是Ex，因为Hy的计算不涉及边界外的节点

取观察点为：$E_x^{n+1/2}(1/2)$

$$\begin{aligned} \frac{E_x^{n+1/2}(1) - E_x^{n+1/2}(0)}{\Delta z} = \frac{E_x^{n+1}(1/2) - E_x^{n}(1/2)}{c \Delta t} \\ \frac{\frac{E_x^{n+1}(1) + E_x^{n}(1)}{2} - \frac{E_x^{n+1}(0) + E_x^{n}(0)}{2}}{\Delta z} = \frac{\frac{E_x^{n+1}(1) + E_x^{n+1}(0)}{2} - \frac{E_x^{n}(1) + E_x^{n}(0)}{2}}{c \Delta t} \\ E_x^{n+1}(0) = E_x^{n}(1) + \frac{c \Delta t - \Delta z}{c \Delta t + \Delta z} [E_x^{n+1}(1) - E_x^n(0)] \\ E_x^{n+1}(0) = E_x^{n}(1) + \alpha [E_x^{n+1}(1) - E_x^n(0)] \\ \end{aligned}$$

对应Fortran代码：

Ex(0, t) = Ex(1, t - 1) + alpha * ( Ex(1, t) - Ex(0, t - 1) )

右边界：

要计算的是Ex，右边界的YEE元胞的Hy分量无需计算

同理有：

$$E_z^{n+1}(i) = E_z^{n}(i-1) + \alpha [E_z^{n+1}(i-1) - E_z^{n}(i)]$$

对应Fortran代码：

Ex(end, t) = Ex(end - 1, t - 1) + alpha * ( Ex(end - 1, t) - Ex(end, t - 1) )

编程求解

代码

program one_dimensional_FDTD_radiation_field
    ! 平面电流源的辐射场分布，边界采用Mur一阶近似吸收边界
    ! 场源位于z=250处，为xoy平面，源为一时谐源：cos(2*pi*3*1e8*t)，区域为真空
    ! z = 0， 500 * deltaZ处采用一阶吸收边界
    real mu_0, epsilon_0, pi, c, delta_z, delta_t, ca, cb, cp, cq, alpha
    real Ex(0:500,0:500), Hy(0:500,0:500) !(z,t)
    integer step, source_z, t, z
    external current_source

    pi = 3.14
    mu_0 = 4 * pi * 1.0e-7
    epsilon_0 = 8.85 * 1.0e-12
    c = 3.0e8
    delta_z = 1.0 / 40.0
    delta_t = delta_z / (2 * c)
    step = 500
    source_z = 250
    ca = 1.0
    cb = (delta_t) / (epsilon_0 * delta_z)
    cp = 1.0
    cq = (delta_t) / (mu_0 * delta_z)
    alpha = (c * delta_t - delta_z) / (c * delta_t + delta_z)

    ! 赋初值
    do i = 0, step
        do j = 0, step
            Ex(i,j) = 0
            Hy(i,j) = 0
        end do
    end do

    ! 主体
    do t = 1, step
        ! 先计算非截断边界处的Ex
        do z = 1, step - 1
            Ex(z,t) = Ex(z, t - 1) - cb * ( Hy(z, t - 1) - Hy(z - 1, t - 1) )
            ! 处理元胞包含电流源时
            if ( z == source_z ) then                
                Ex(z,t) = Ex(z,t) - cb * current_source( (t + 0.5) * delta_t )                
            end if
        end do
        ! 处理边界 Mur一阶近似吸收边界
        Ex(0, t) = Ex(1, t - 1) + alpha * ( Ex(1, t) - Ex(0, t - 1) )
        Ex(step, t) = Ex(step - 1, t - 1) + alpha * ( Ex(step - 1, t) - Ex(step, t - 1) )
        ! Hy分量 z = 0时 Hy(z + 1/2)的计算不涉及截断边界以外的计算
        do z = 0, step - 1
            Hy(z,t) = cp * Hy(z, t - 1) - cq * ( Ex(z + 1, t) - Ex(z, t) )
        end do
    end do
    
    ! 数据整理
    open(6,file='electric_field_FDTD_solution_while_step_t_400.dat')
    open(7,file='electric_field_analytic_solution_while_step_t_400.dat')
    open(8,file='compare_analytic_solution_and_FDTD_solution_while_step_t_400.dat')
    do z = 0, step
        write(6, *)z, Ex(z, 400) ! t=400*delta_t时的由FDTD解出的Ex
        temp = electric_field_analytic_solution(400.0 * delta_t, z * delta_z, c) ! t=400*delta_t时的由解析解解出的Ex
        write(7, *)z, temp
        write(8, *)z, Ex(z, 400), temp
    end do
    
end program one_dimensional_FDTD_radiation_field

!电流源
function current_source(t)
    real pi, current_source, t
    pi = 3.14
    current_source = cos(2 * pi * 3 * 1e8 * t)
    return
end

!由解析式求得的精确解
function electric_field_analytic_solution(t, z, v)
    real pi, impedance, electric_field_analytic_solution, t, z, v
    external current_source
    pi = 3.14
    impedance = 120.0 * pi !波阻抗
    electric_field_analytic_solution = (impedance / 2) * current_source(t - z / v)
    return
end

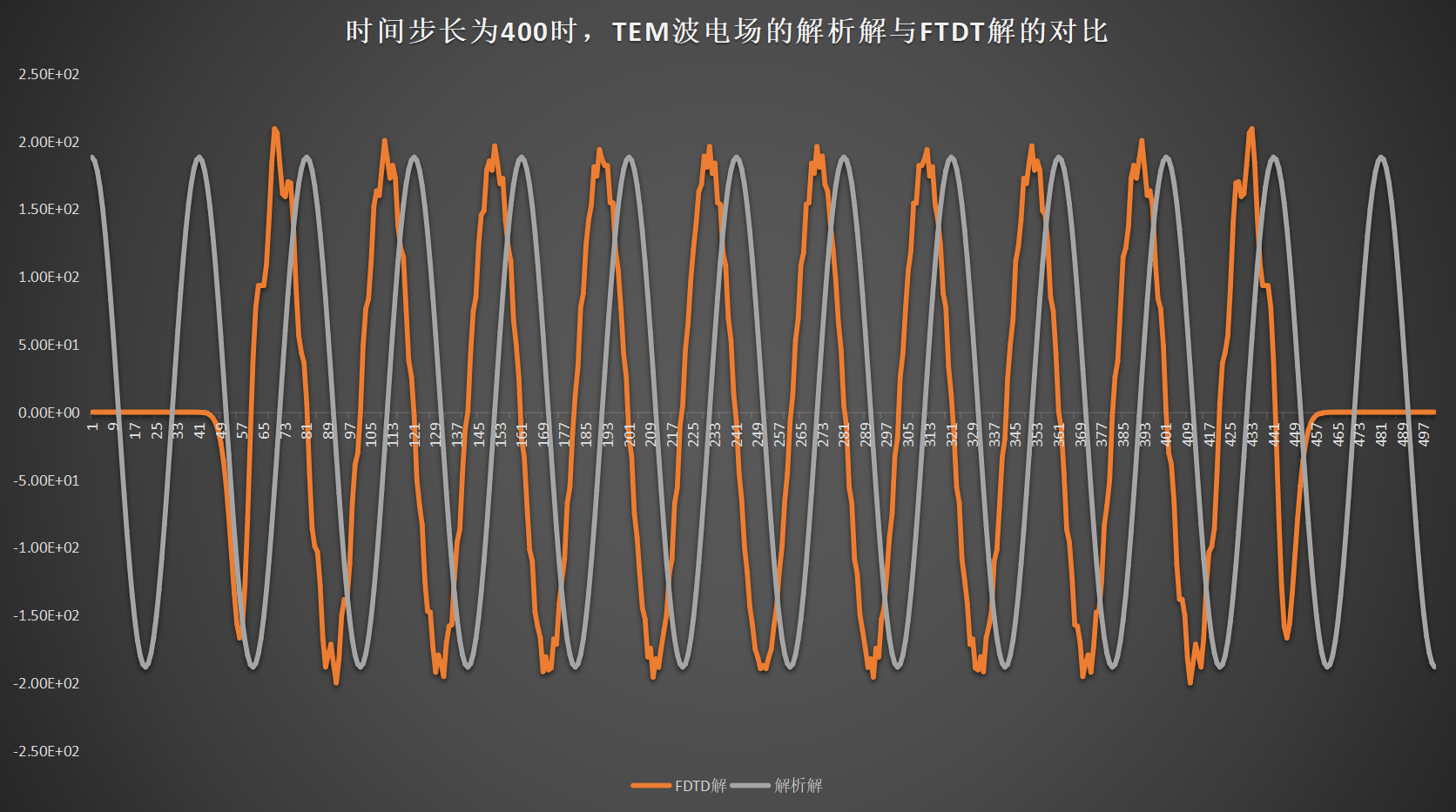
结果分析