FDTD基本公式

Maxwell方程和Yee元胞

选择Maxwell的旋度方程：

$\left\{ \begin{array}{a} \nabla \times \vec{E} + \frac{\partial \vec{B}}{\partial t} = -\vec{J_m} \\ \nabla \times \vec{H} - \frac{\partial \vec{D}}{\partial t} = \vec{J} \\ \end{array} \right. \tag {1-1}$

注意到这里带上了$\vec{J_m}$，这是考虑到在磁介质中，有磁电流的存在。

线性各项同性介质中，本构关系为：

$\left\{ \begin{array}{} \vec{D} = \epsilon \vec{E} \\ \vec{H} = \mu \vec{B} \\ \vec{J} = \sigma \vec{E} \\ \vec{J_m} = \sigma_m \vec{H} \end{array} \right. \tag {1-2}$

选取直角坐标系：

$\begin{cases} \frac{\partial E_z}{\partial y} - \frac{\partial E_y}{\partial z} & = -\mu \frac{\partial H_x}{\partial t} - \sigma_m H_x \\ & \vdots \\ \frac{\partial H_z}{\partial y} - \frac{\partial H_y}{\partial z} & = \epsilon \frac{\partial E_x}{\partial t} + \sigma E_x \\ & \vdots \\ \end{cases} \tag {1-3}$

有微分形式了就可以试试有限差分了。

YEE元胞离散

是一个边长为$\Delta$的正方形，将空间使用Yee元胞充填。

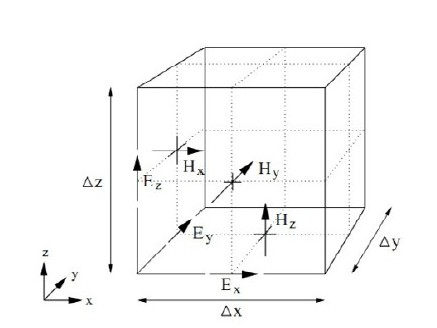
待补充描述

记：

$f^n(i,j,k) = f(i\Delta x, j\Delta y, k\Delta z, n\Delta t)$

在空间和时间取样上，电场磁场的分布如下表：

$\begin{array}{c} % 总表格 \begin{array}{cc} % 第一行内分成两列 \begin{array}{|c|c|c|c} % 第一列"最小值"数组 & x & y & z & t\\ \hline E_x & i + 1/2 & j & k & n & \\ \hline E_y & i & j + 1/2 & k & n & \\ \hline E_z & i & j & k + 1/2 & n & \\ \hline H_x & i & j + 1/2 & k + 1/2 & n + 1/2 & \\ \hline H_y & i + 1/2 & j & k + 1/2 & n + 1/2 & \\ \hline H_z & i + 1/2 & j + 1/2 & k & n + 1/2 & \\ \end{array} \end{array} % 第一行表格组结束 \end{array} % 总表格结束$

这里提一个，初看可能不会注意的点：举例来说，$E^n_x(i+1/2,j,k)$和$H^{n+1/2}_x(i,j+1/2,k+1/2)$是同级的

对有限差分，空间与时间都取一阶近似：

$\begin{align} & \left. \frac{\partial f^n(i,j,k)}{\partial x} \right| _{x = i\Delta x} \approx \frac{f^n(i + 1/2,j,k) - f^n(i - 1/2,j,k)}{\Delta x} \\ & \vdots \\ & \left. \frac{\partial f^n(i,j,k)}{\partial t} \right| _{t = n\Delta x} \approx \frac{f^{n + 1/2}(i,j,k) - f^{n - 1/2}(i,j,k)}{\Delta t} \\ \end{align} \tag {1-4}$

直角坐标系下三维空间的FDTD公式

这里我先选择求解磁场分量，以x轴分量为例。先求解磁场分量，可能会产生一个不好的概念，先看下去。

要求解$H^{n+1/2}_x(i,j+1/2,k+1/2)$，即n时刻的(i,j,k)元胞，注意这里我提及的为n时刻而非n+1/2时刻，这只是为了以后编程方便（n，n+1/2是同级的）。

取$H_x(i,j+1/2,k+1/2, n\Delta t)$为观察点（这个选点很妙！）

对直角坐标系下的Maxwell方程组：$\frac{\partial E_z}{\partial y} - \frac{\partial E_y}{\partial z} = -\mu \frac{\partial H_x}{\partial t} - \sigma_m H_x$

以观察点为中心点，进行差分。

$\begin{align} & \frac{E^n_z(i,j+1,k) - E^n_z(i,j,k)}{\Delta y} - \frac{E^n_y(i,j,k+1) - E^n_y(i,j,k)}{\Delta z} \\ = & -\mu(i,j+1/2,k+1/2) \frac{H^{n+1/2}_x(i,j+1/2,k+1/2) - H^{n-1/2}_x(i,j+1/2,k+1/2)}{\Delta t} - \sigma_m(i,j+1/2,k+1/2) H^{n}_x(i,j+1/2,k+1/2) \\ \end{align} \tag {1-5}$

对观察点取两点平均近似：

$H^{n}_x(i,j+1/2,k+1/2) = \frac{H^{n+1/2}_x(i,j+1/2,k+1/2) + H^{n-1/2}_x(i,j+1/2,k+1/2)}{2} \tag {1-6}$

记标号：$l = (i,j+1/2,k+1/2)$

则式（1-5）右端：

$\begin{align} & -\mu(l) \frac{H^{n+1/2}_x(l) - H^{n-1/2}_x(l)}{\Delta t} - \sigma_m(l) H^{n}_x(l) \\ = & -\left[ \frac{\mu(l)}{\Delta t} + \frac{\sigma_m(l)}{2} \right] H^{n+1/2}(l) - \left[\frac{\sigma_m(l)}{2} - \frac{\mu(l)}{\Delta t} \right] H^{n-1/2}(l) \\ \end{align} \tag {1-7}$

最后可得：

$\begin{align} H_x^{n+1/2}(l) & = CP(l) H^{n-1/2}(l) \\ & - CQ(l) \left[ \frac{E^n_z(i,j+1,k) - E^n_z(i,j,k)}{\Delta y} - \frac{E^n_y(i,j,k+1) - E^n_y(i,j,k)}{\Delta z} \right] \\ \end{align} \tag {1-8}$

其中：

$CP(l) = \frac{\frac{\mu(l)}{\Delta t} - \frac{\sigma_m(l)}{2}}{\frac{\mu(l)}{\Delta t} + \frac{\sigma_m(l)}{2}} \quad CQ(l) = \frac{1}{\frac{\mu(l)}{\Delta t} + \frac{\sigma_m(l)}{2}} \tag {1-9}$

如此取其他位置的磁场分量作为观察节点，空间上Yee元胞的磁场分布：

$\vec{H}_x^{n+1/2}(i,j+1/2,k+1/2) ,\quad \vec{H}_z^{n+1/2}(i+1/2,j,k+1/2) ,\quad \vec{H}_x^{n+1/2}(i+1/2,j+1/2,k) ,\quad \tag {1-10}$

这里注意，要求出$H^{n+1/2}$，需要的值为：上一个时刻的磁场分量，以及同时刻的电场分量。（这里可能会产生一个不好的概念）

如何去理解呢？

从编程的角度来说，在时间循环语句中，假设此时正在计算n时刻的YEE元胞，此时要计算出的正是E[n] H[n+1/2]但是对于计算机来说，数组的标号都是n，即计算E[n] H[n]。我写这么啰嗦就是因为之前编程计算时犯错了，以为H[n+1/2]对应的下标为[n+1]。这就是为什么我说n，n+1/2是同级的。

同理我们取第n+1/2时刻的电场作为观察节点，也可解得电场分布。

如取$E^{n+1/2}_x(i+1/2,j,k)$

$\begin{align} E_x^{n+1}(l) & = CA(l) E^{n}(l) \\ & + CB(l) \left[ \frac{H^{n+1/2}_z(i+1/2,j+1/2,k) - H^{n+1/2}_z(i+1/2,j-1/2,k)}{\Delta y} - \frac{H^{n+1/2}_y(i+1/2,j,k+1/2) - H^{n+1/2}_y(i+1/2,j,k-1/2)}{\Delta z} \right] \\ \end{align} \tag {1-11}$

其中：

$l = (i+1/2,j,k) ,\quad CA(l) = \frac{\frac{\epsilon(l)}{\Delta t} - \frac{\sigma(l)}{2}}{\frac{\epsilon(l)}{\Delta t} + \frac{\sigma(l)}{2}} \quad CB(l) = \frac{1}{\frac{\epsilon(l)}{\Delta t} + \frac{\sigma(l)}{2}} \tag {1-12}$

这里给出汇总：

$\begin{cases} \vec{E}^{n+1} = CA \cdot \vec{E}^{n} + CB \left[ \nabla \times \vec{H} \right]^{n+1/2} \\ \vec{H}^{n+1/2} = CP \cdot \vec{H}^{n-1/2} - CQ \left[ \nabla \times \vec{E} \right]^{n} \\ \end{cases}$

这里可以看出在编程计算中，我们应该先求解全空间的E[n]后再求解H[n]

二维问题

物理量与z坐标无关，即$\frac{\partial}{\partial z} = 0$

就分为TE波与TM波

TE波

TE波的特点为：$H_z \neq 0 \quad E_z = 0$
TM波

TM波的特点为：$E_z \neq 0 \quad H_z = 0$

一维问题

看作沿着z轴传播的TEM波，即：$\frac{\partial}{\partial x} = 0 \quad \frac{\partial}{\partial y} = 0 \quad E_z = 0 \quad H_z = 0$

时间离散程度和空间离散程度对稳定性影响的讨论

时间上（亦或是数值稳定条件）

对时谐场$f(x,y,z,t) = A(x,y,z) \exp{(\jmath \omega t)}$。考虑一定点$f = f_0 \exp{(\jmath \omega t)}$，进行时间离散，一阶中心差分。

$\jmath \omega f^n = \frac{\partial f}{\partial t} = \frac{f^{n+1/2} - f^{n-1/2}}{\Delta t} \tag {1-13}$

增长因子

定义增长因子$q{numerical}$，简称$q{num}$

$q_{num} = \frac{f^{n+1/2}}{f^n} = \frac{f^n}{f^{n-1/2}} \tag {1-14}$

带回（1-13）：

$q^2_{num} - \jmath \omega \Delta t q_{num} - 1 = 0 \tag {1-15}$

由其解为：

$q_{num} = \frac{\jmath \omega \Delta t }{2} \pm \sqrt{1 - (\frac{\omega \Delta t}{2})^2} = |{q_{num}}| \exp{(\jmath \psi_{num})} \tag {1-16}$

而由其定义可得：

$q_{num} = \frac{f^{n+1/2}}{f^n} = \frac{f_0 \exp{(\jmath \omega (n+1/2)\Delta t)}}{f_0 \exp{(\jmath \omega n\Delta t)}} = exp{(\frac{\jmath \omega}{2} \Delta t)} \tag {1-17}$

所以式（1-16）一定要满足式（1-17）。即模值为1，相移为$\frac{\omega \Delta t}{2}$。

模值条件

首先满足模值为1。$|q_{num}| = 1$

由式（1-16）：

$|q_{num}| = \sqrt{1 - (\frac{\omega \Delta t}{2})^2 + (\frac{\omega \Delta t}{2})^2} = 1 \tag {1-18}$

但为了满足（1-18），必须要：

$1 - (\frac{\omega \Delta t}{2})^2 \ge 0 \Rightarrow \Delta t \le \frac{2}{\omega} = \frac{T}{\pi} \tag {1-19}$

若离散间隔过大，不满足（1-19），则$q_{num}$为纯虚数，其模值：

$|q_{num}| = \sqrt{\left[ \frac{\omega \Delta t }{2} \pm \sqrt{(\frac{\omega \Delta t}{2})^2 - 1} \right]^2} \tag {1-20}$

要其模值为1，解之得$\frac{\omega \Delta t }{2} = 1$或$\frac{\omega \Delta t }{2} = 0$，这在$q_{num}$为纯虚数的条件下，这些解都不成立。
模值不为1，则进行差分获得的数值解就会趋于发散或衰减

相位条件

满足相移$\frac{\omega \Delta t}{2}$

由式（1-16）：

$\psi_{num} = \arctan{ \frac{ \pm \frac{\omega \Delta t}{2} }{ \sqrt{1 - (\frac{\omega \Delta t}{2})^2} } } \tag {1-21}$

在$\frac{\omega \Delta t}{2}$取值足够小时，有近似：

$\frac{ 1 }{ \sqrt{1 - (\frac{\omega \Delta t}{2})^2} } \approx 1 + \frac{1}{2} (\frac{\omega \Delta t}{2})^2 \quad ((1+bx)^a \backsim 1 + bax) \tag {1-22}$

由此有：

$\psi_{num} \approx \arctan{ \frac{\omega \Delta t}{2} \left[ 1 + \frac{1}{2} (\frac{\omega \Delta t}{2})^2 \right] } \tag {1-23}$

如果把$\frac{\omega \Delta t}{2}$看作无穷小，则$(\frac{\omega \Delta t}{2})^2$就是更高阶的无穷小。则有近似：

$\psi_{num} \approx \arctan{ \frac{\omega \Delta t}{2} } \tag {1-24}$

对无穷小近似有：

$\arctan{\Delta x} \approx \Delta x \tag {1-25}$

在三角函数中（我感觉是实际运用中），在$\Delta x \le \frac{\pi}{10}$时，即18度时，有（1-25）的近似，那么我们就可得相位条件：

$\frac{\omega \Delta t}{2} \le \frac{\pi}{10} \Rightarrow \Delta t \le \frac{T}{10} \tag {1-26}$

时间离散要求

（1-26）比（1-19）要更为严格，我们采用（1-26）

空间上（亦或是色散稳定条件）

先考虑一维情形

书上说：从Maxwell方程可导出电磁场任意直角分量均满足齐次波动方程。
$\frac{\partial^2 f}{\partial x^2} + \frac{\omega^2}{c^2}f = 0$
我觉得，首先这是限定在无源空间下，等式右边才会为0。在时谐电磁场下，才会有等式左边的形式。

直接来

$\frac{\partial^2 f}{\partial x^2} + \frac{\omega^2}{v^2} f = 0 \tag {1-27}$

仅考虑向x正方向，解得：

$f(x,t) = f_0 \exp{ [ \jmath (\omega t - kx) ] } \quad , k = \frac{\omega}{v} \tag {1-28}$

相速度：

$v_p = \frac{\omega}{k} \tag {1-29}$

理论上相速度应与频率无关。那么对差分计算得出的结果也应满足这个结论。由（1-27）带入中心差分公式：

$\begin{align*} \frac{ f(x + \Delta x, t) - 2f(x,t) + f(x - \Delta x, t) }{(\Delta x)^2} + \frac{\omega^2}{v^2} f(x,t) & = 0 \\ \frac{ f(x,t) \cdot [\exp{ (\jmath k \Delta x) } + \exp{ (-\jmath k \Delta x) } - 2] }{(\Delta x)^2} + \frac{\omega^2}{v^2} f(x,t) & = 0 \\ \frac{ 2\cos{ (k \Delta x) } - 2 }{(\Delta x)^2} + \frac{\omega^2}{v^2} & = 0 \\ \end{align*} \tag {1-30}$

若$k\Delta x)$足够小，有Taylor近似，我们仍然有（1-29），如果过大，那么相速度就和频率有关了，就会造成色散。（还是那个）$k\Delta x \le \frac{\pi}{10}$时：

$\cos{ (k \Delta x) } - 1 \approx -\frac{1}{2} (k\Delta x)^2 \tag {1-31}$

即得到：

$k\Delta x \le \frac{\pi}{10} \Rightarrow \Delta x \le \frac{\lambda}{20} \tag {1-32}$

其实可以更小：（我给的近似关系应该错了，用二倍角公式把cos转成sin那个近似关系才能用）真实应该是：

$\Delta x \le \frac{\lambda}{10} \tag {1-33}$

更高维同理。

如果我们对时谐电磁场采用时域上的齐次波动形式：

$\frac{\partial^2 f}{\partial x^2} - \frac{1}{v} \frac{\partial^2 f}{\partial t^2} = 0 \tag {1-34}$

可推出色散稳定条件对时间离散的要求：

一维空间上

$(\frac{\omega \Delta t}{2})^2 \le 1 \Rightarrow \Delta t \le \frac{2}{\omega} = \frac{T}{\pi} \tag {1-35}$

就如同（1-19）。

Courant稳定性条件

给出时间间隔和空间间隔的互相制约关系。

无界域中无源的时谐电磁场满足齐次波动方程：

$\nabla^2 f + \frac{\omega^2}{v^2} f = 0 \tag {1-36}$

代入中心差分公式，和上面的空间要求的推导差不多：

$\frac{ \sin^2{ (\frac{k_x \Delta x}{2}) } }{ (\frac{\Delta x}{2})^2 } + \frac{ \sin^2{ (\frac{k_y \Delta y}{2}) } }{ (\frac{\Delta y}{2})^2 } + \frac{ \sin^2{ (\frac{k_z \Delta z}{2}) } }{ (\frac{\Delta z}{2})^2 } - \frac{\omega^2}{v^2} = 0 \tag {1-37}$

防止色散的出现，时间离散和空间离散在上一节已经讨论过，但他们的相对关系其实就是一维空间上色散稳定条件对时间离散的要求的拓展。

有：

时间间隔必定要满足（1-35）。有不等式：

放缩一下：

$(\frac{v \Delta t}{2})^2 \left[ \frac{ \sin^2{ (\frac{k_x \Delta x}{2}) } }{ (\frac{\Delta x}{2})^2 } + \frac{ \sin^2{ (\frac{k_y \Delta y}{2}) } }{ (\frac{\Delta y}{2})^2 } + \frac{ \sin^2{ (\frac{k_z \Delta z}{2}) } }{ (\frac{\Delta z}{2})^2 } \right] \le (\frac{v \Delta t}{2})^2 \left[ \frac{ 1 }{ (\frac{\Delta x}{2})^2 } + \frac{ 1 }{ (\frac{\Delta y}{2})^2 } + \frac{ 1 }{ (\frac{\Delta z}{2})^2 } \right] \le 1 \tag {1-40}$

得：

$v \Delta t \le \frac{1}{ \sqrt{ (\frac{1}{\Delta x})^2 (\frac{1}{\Delta y})^2 (\frac{1}{\Delta z})^2 } } \tag {1-41}$

对Yee元胞：

$v \Delta t \le \delta \tag {1-42}$

即时间间隔必须小于或等于波通过一维Yee元胞所用的时间。

各向异性

不推了。。。。减小各向异性，对空间离散度的要求：

$\delta \lt \frac{\lambda}{8} \tag {1-43}$