查找 | MH's Blog

说明一下数组长度为n，是从1-n，0的位置拿来做哨兵

查找表

概念

同一类型的数据元素构成的集合
含有的操作有
1. 查询某个特定的元素是否在表中
2. 检索某个特定元素的各种属性
3. 插入或删除某个元素

将含有插入删除操作的查找表称为动态查找表，只有1,2的称为静态查找表

关键字概念(Key)

数据元素某个数据项的值
如果该关键字可以唯一的标识这个元素，称为主关键字 否则为次关键字

操作

Creat
Destroy
Search
Traverse

查找的性能分析

ASL:平均查找长度

成功时平均查找长度
失败时平均查找长度

$ASL=\sum_{i=1}^n{P_iC_i}$
$P_i$为查找第i个元素的概率$C_i$为找到与key相等时比较的次数(针对成功查找而言)

查找

顺序表的查找

顺序表：顺序存储

int SearchSeq(int array[], int key, int length)
{
    array[0] = key;
    for (int i = length; array[i] != key; --i)
        ;
    return 0;
}

分析ASL
成功：$P_i=1\; C_i=n-i+1\; ASL=\frac{n+1}{2}$
失败：$P_i=1\; C_i=n\; ASL=n$

优化：把被查找概率大的元素放比较早被比较对被概率不相等时

有序表的查找

表内元素有序排列(递增，递减都可)
用递增做例子
可采用顺序查找,加个判断大小

折半查找

仅适用于有序的 顺序表

int SearchBin(int array[], int key, int length)
{
    int low = 1, height = length;
    while (low < height)
    {
        int mid = ((height - low) >> 1) + low;
        if (array[mid] == key)
        {
            return mid;
        }
        else if (array[mid] < key)
        {
            low = mid + 1;
        }
        else
        {
            height = mid + 1;
        }
    }
    return 0;
}

循环跳出条件为l> 1) + low是向下取整的，也就是在区间有偶数个元素时说左边比右边少一个元素

对折半查找的分析

就算把表划分成了一个完全二叉树(编号与位置相同)
对一棵有n个节点的完全二叉数的高度$h=[log_2n]+1$,因此折半查找最多对比h次

查找成功时
$ASL=\frac{1}{n}\sum_{i=1}^{h}{i*2^{i-1}} \leq \frac{h}{n}\frac{1-2^h}{1-2}=O(log_2n)$
课本上给了一个一个更好的证明$ASL=\frac{n+1}{n}log_2(n+1)-1$
有h层，第i层的查找长度为i，且第i层有$2^{i-1}$个节点当然这个节点数是对满二叉树而言
查找失败时
失败的可能为n+1种情况，因为n个数划分出了n+1个区间,每一次都要比较h次 $ASL=h(n+1)$

时间复杂度$O(log_2n)$

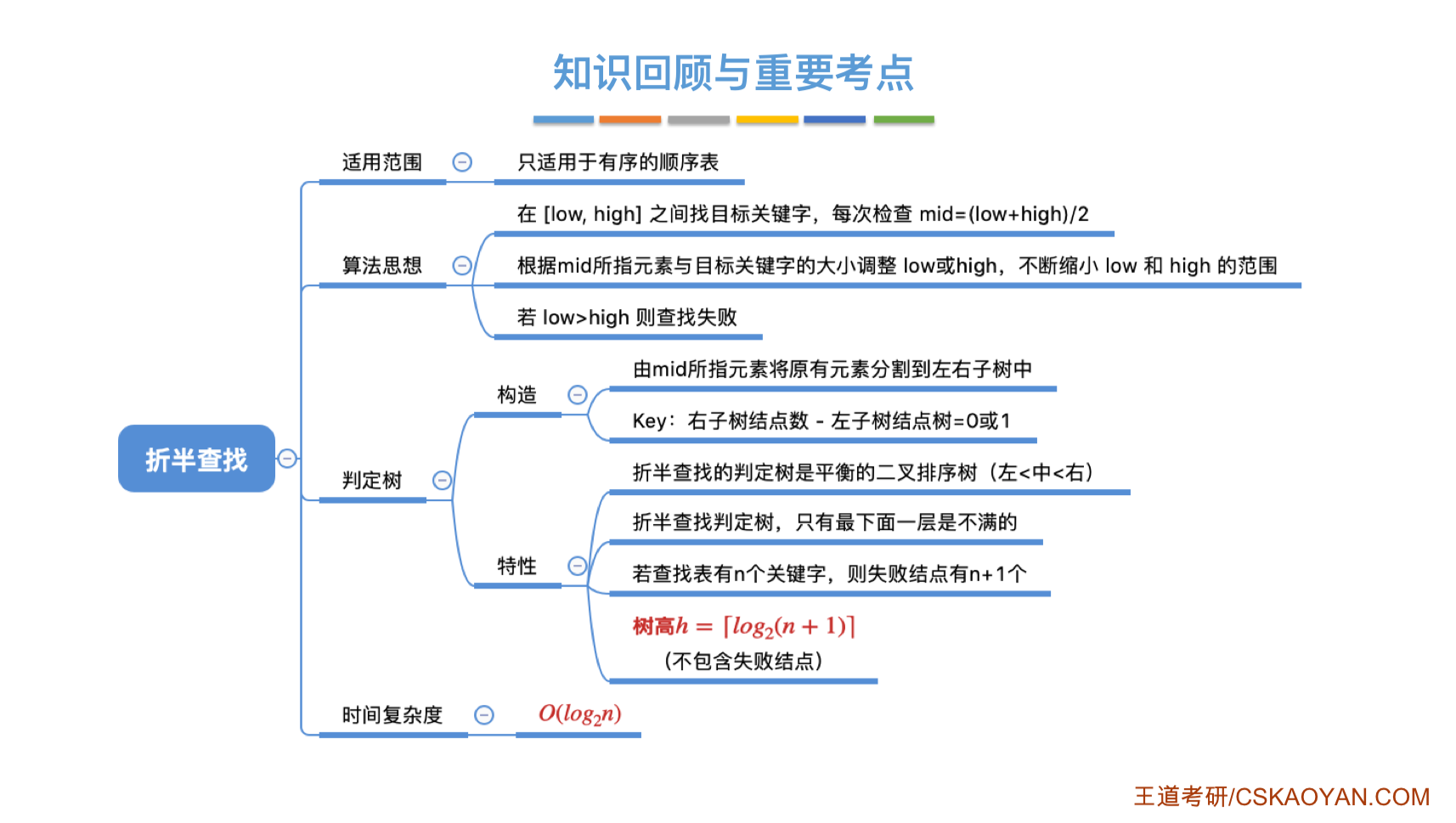
分块查找

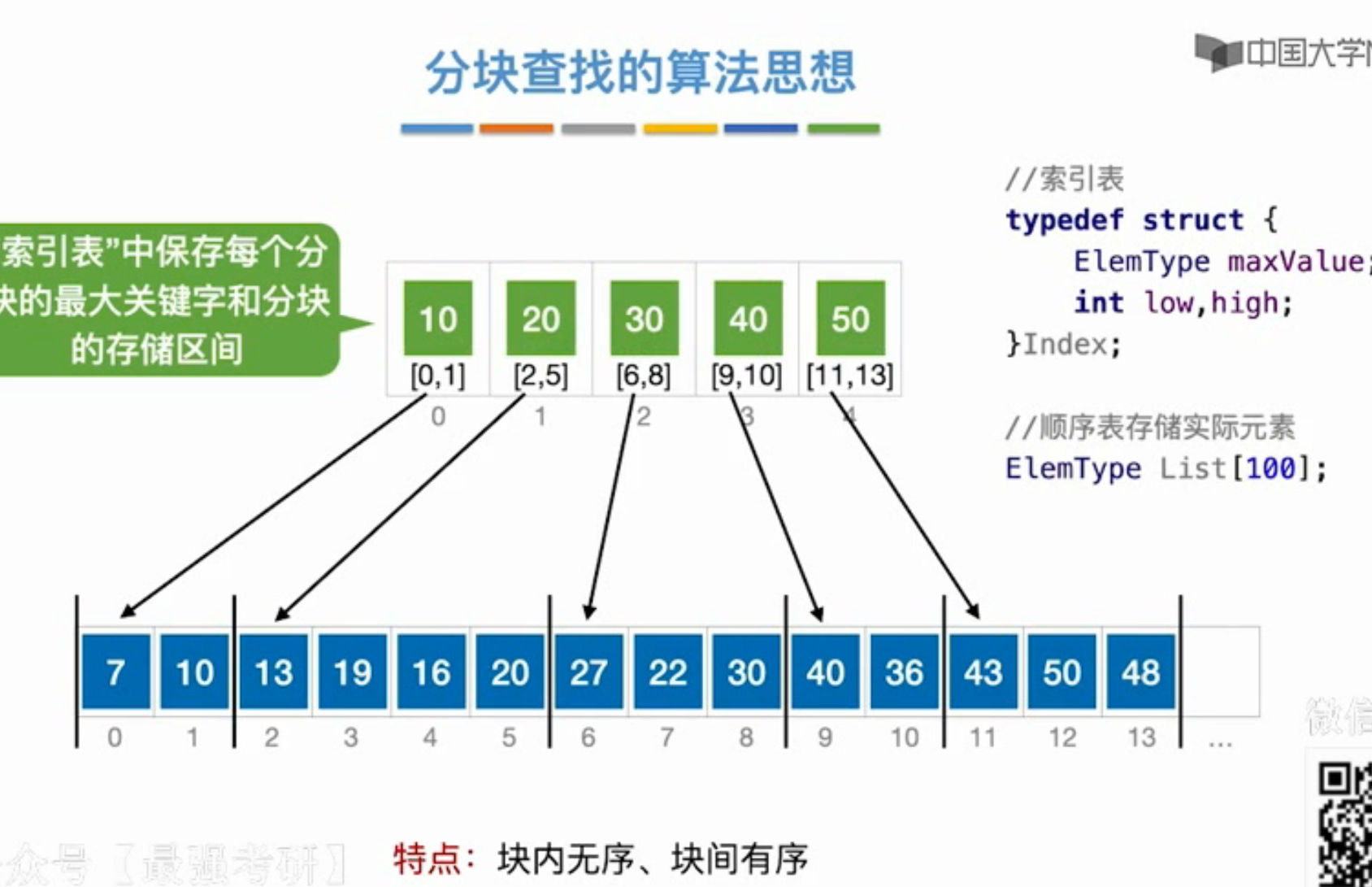
索引顺序查找
先在索引表中确定代查元素所属分块，再在分块内找

用折半查找查找索引

难点在于给出的key不一定在索引表中，要根据索引表的性质判断key可能在的区块
key在索引表中时：拿到区块后，再去区块中寻找
key不在索引表中时：首先假设key对应区块的最大值为maxVal，$key<maxVal$,所以折半查找的最后一步一定是heigh=mid-1; 倒数第二步一定是l=h=mid,对应的区块一定为low指向的区间，当然这key没有大于表里最大值的情况，如果key比表中最大值还大，那么最后一定是low超出界限，所以也要用low

$ASL=L_i+L_s$ 只考虑成功情况下

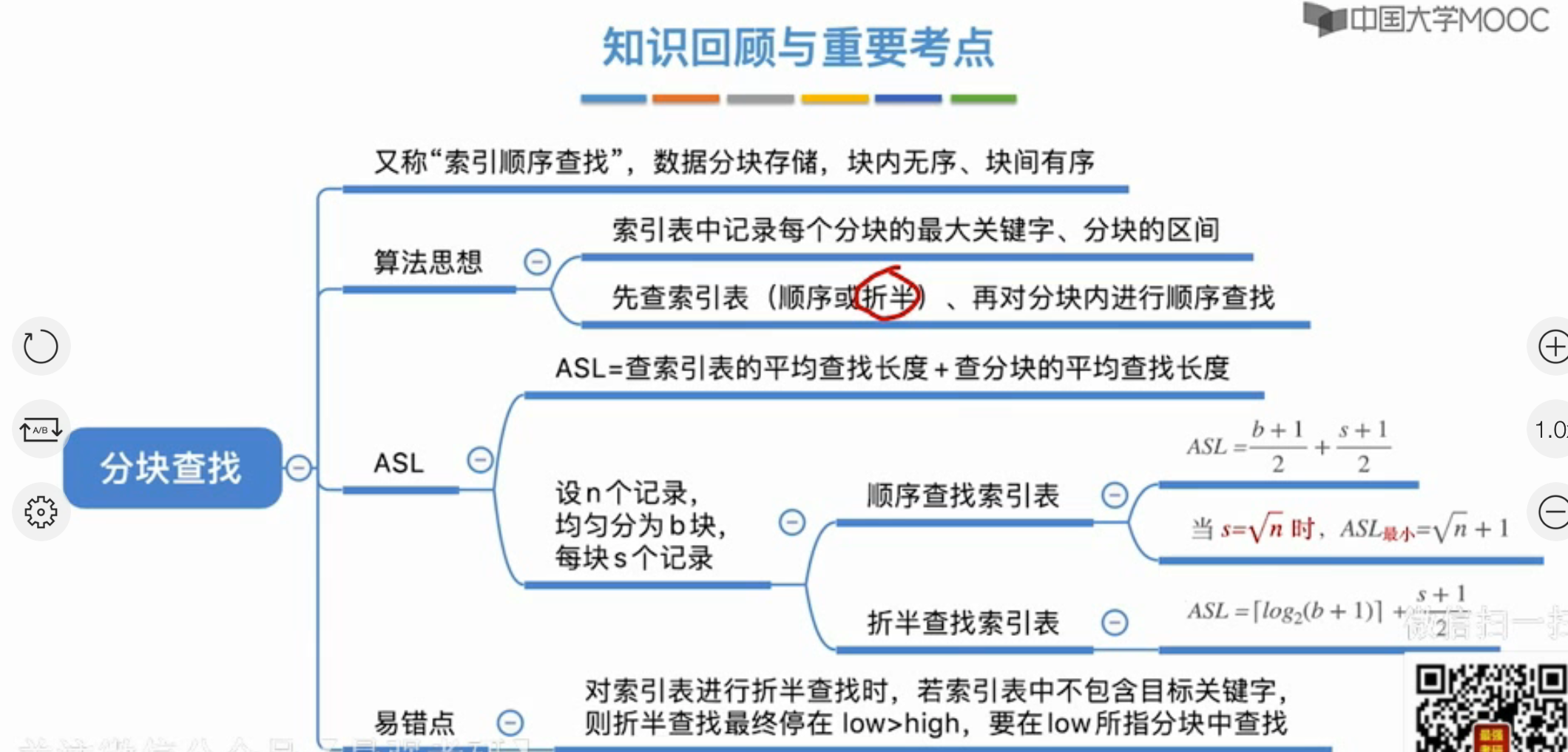
B树(只要求会手算)

m阶B树
如果不是空树这一定要满足

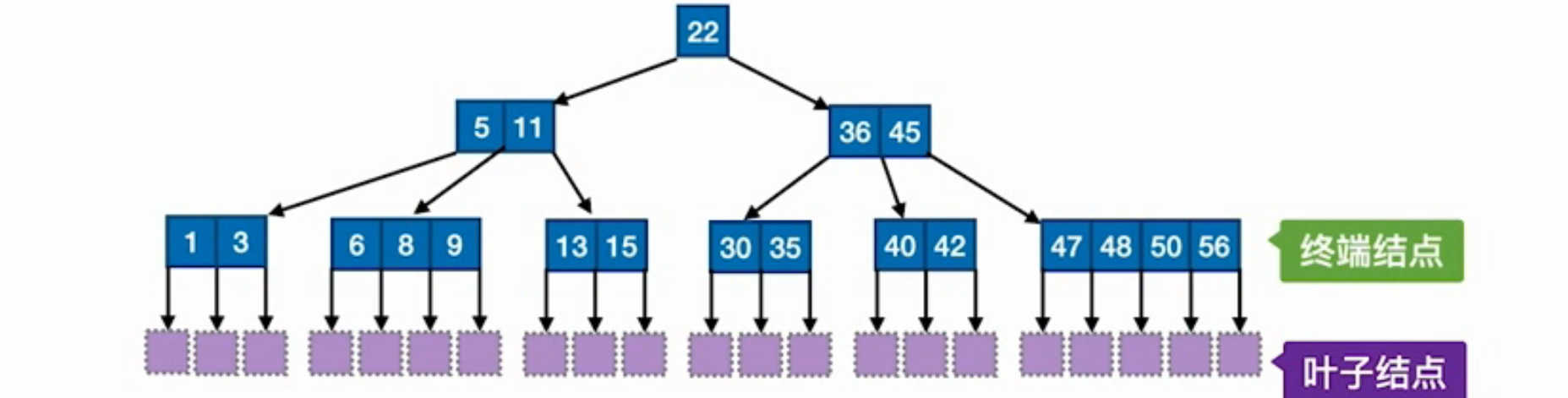
性质

一个结点(不是根节点)含有的子树数量$\in [[m/2],m]$，含有的关键字数量$\in [[m/2]-1,m-1]$ 注意这里的取整函数是向上取整的！！
若根结点不是终端结点，则至少有两棵子树，即子树数量$\in [2,m]$，关键字数量$\in [1,m-1]$
任一一个结点，其子树高度都相同，即极度平衡完全平衡
叶子结点不带信息
关键字大小排列：子树0<关键字0<子树1。。。

注意终端结点和叶子结点的区别

叶子结点代表失败情况为n+1种

对B树的树高进行分析

n个key的m阶B树,注意高度一般不包括叶子结点

最大高度$h_{max}$

最大高度要求结点含的元素尽可能的少
第i层含有的子树$l_i$且假定$l_0=1$
第i层含有的结点数为$p_i$
第i层含有的key$k_i$

$p_i=l_{i-1} \\ l_i=p_i*[m/2] \\ k_i=p_i*([m/2]-1) \; i \gt 1$

有：

$\begin{aligned} & l_i=2*[m/2]^{i-1} \Rightarrow \\ n & = \sum_{i=1}^{h_{max}}{p_i*([m/2]-1)} \\ & = 1+\sum_{i=1}^{h_{max}-1}{(l_i*([m/2]-1))} \\ & = 1+2*([m/2]-1)*\frac{1-[m/2]^{h_{max}-1}}{1-[m/2]} \\ & \Rightarrow h_{max}=log_{[m/2]}{\frac{n+1}{2}}+1 \end{aligned}$

这也太傻了，用叶子结点算:

$p_{h_{max}+1}=n+1 \rightarrow n+1 = 2*[m/2]^{h_{max}-1} \rightarrow h_{max} = log_{[m/2]}{\frac{n+1}{2}}+1$

最小高度$h_{min}$

要求结点含的元素尽可能的多。类似于m叉树

$l_i=m^i\; n=(m-1)+\sum_{i=1}^{h_{min}-1}(m-1)l_i=(m-1)\sum_{i=0}^{h_{min}-1}m^i \rightarrow h_{min}=log_m(n+1)$ $log_m(n+1) \le h \le log_{[m/2]}{(\frac{n+1}{2})}+1$

B树的插入删除

插入

先插入吧，插入一个元素一定是在终端结点插入，插入到非终端结点也能被等效到插入终端结点

几种插入情况

不溢出
插入结点key个数$\in[[m/2],m]$
不做调整
溢出
key个数为m个
取中间位置，位置是从1-m，中间位位置[m/2]还是向上取整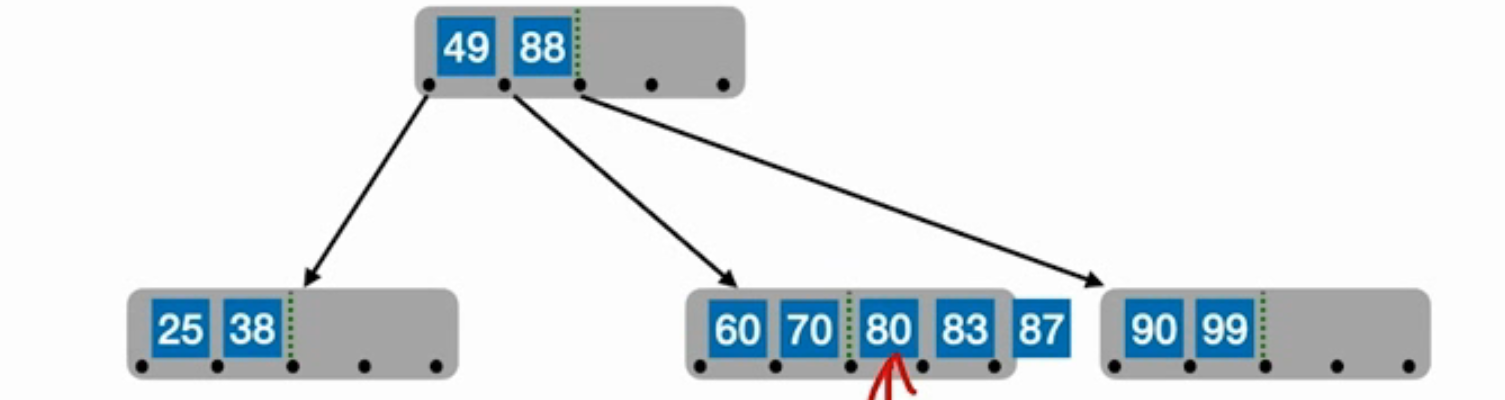

如图插入87，那么应该把80移动到父结点那，83、87成为一个新的结点，与80的右子树相连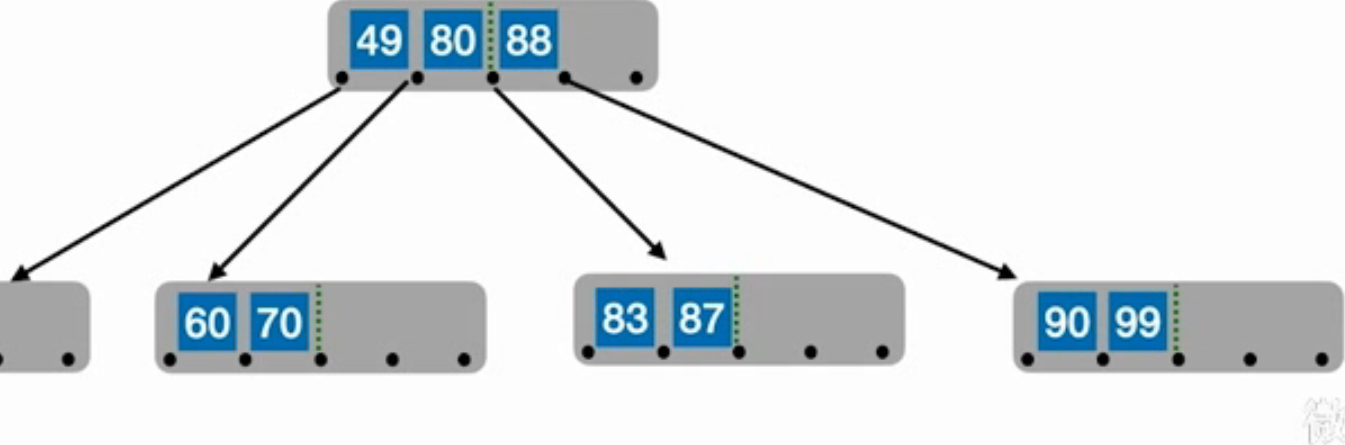

但是如果父结点也溢出了怎么办？
父结点也进行尚书步骤，把一个结点扔给父父结点，分裂。一直重复，该操作有可能使得树的高度加一。

删除

删除一个非终端结点等价于用直接前驱或直接后继代替他的位置，然后删除原来的直接前驱或直接后继
直接前驱或直接后继肯定是终端结点了
非终端结点的

只看删除终端结点就好了而且只用看结点只有[m/2]-1个key的情况

删除后不满足性质了，得去用一个直接前驱或直接后继去填补这个位置

右兄弟够借
用它的后继代替它，再用后继的后继代替后继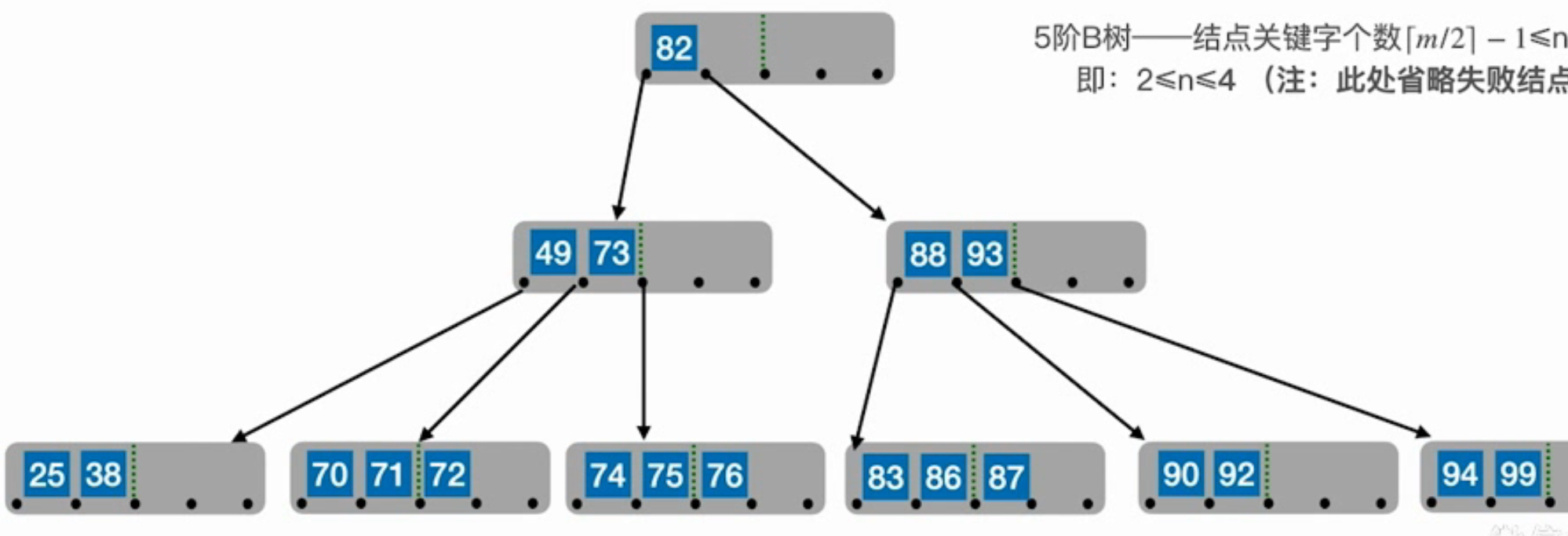

删除25,用49去填补空缺，再用70去填补父结点的空缺
左兄弟够借
用它的前驱代替它，再用前驱的前驱代替前驱
都不够借

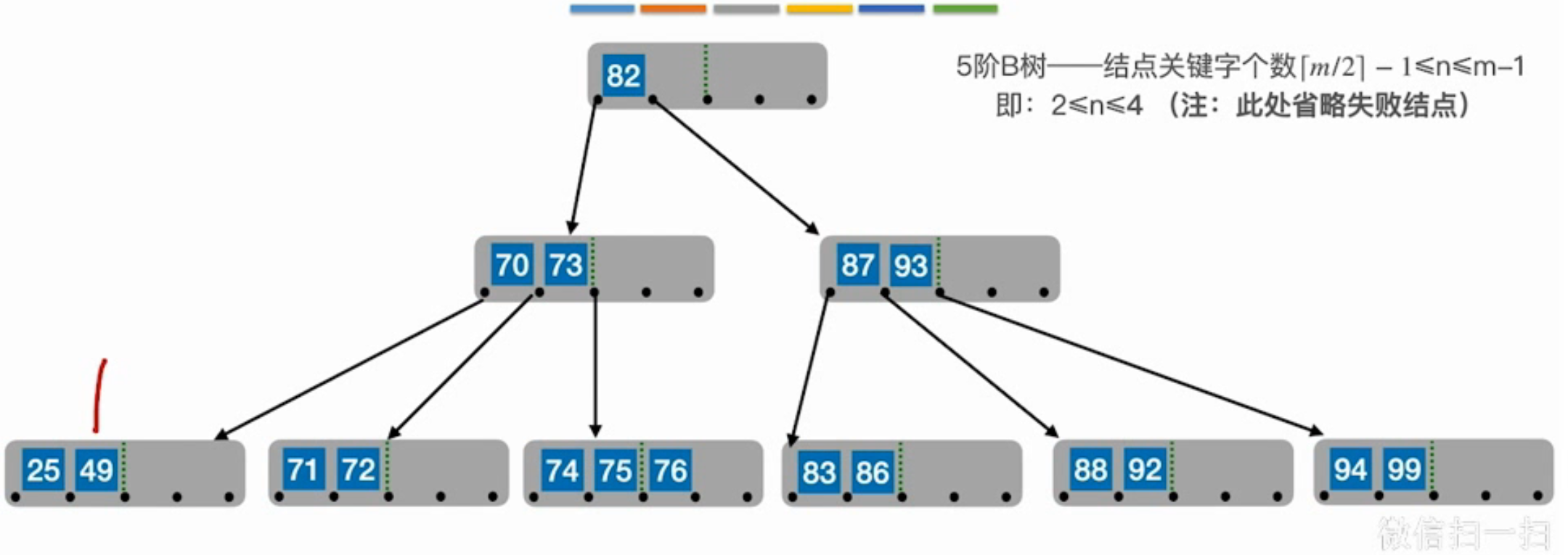
可以将该结点与左(右)兄弟以及连接他们的父结点的key合并成一个结点。如果结束后父结点不满足性质，且父结点的兄弟也不够用，重复之前的步骤，直至满足性质，或者达到根结点，把根结点合并成另一个新结点作为新结点，如果合并到根结点树的高度减1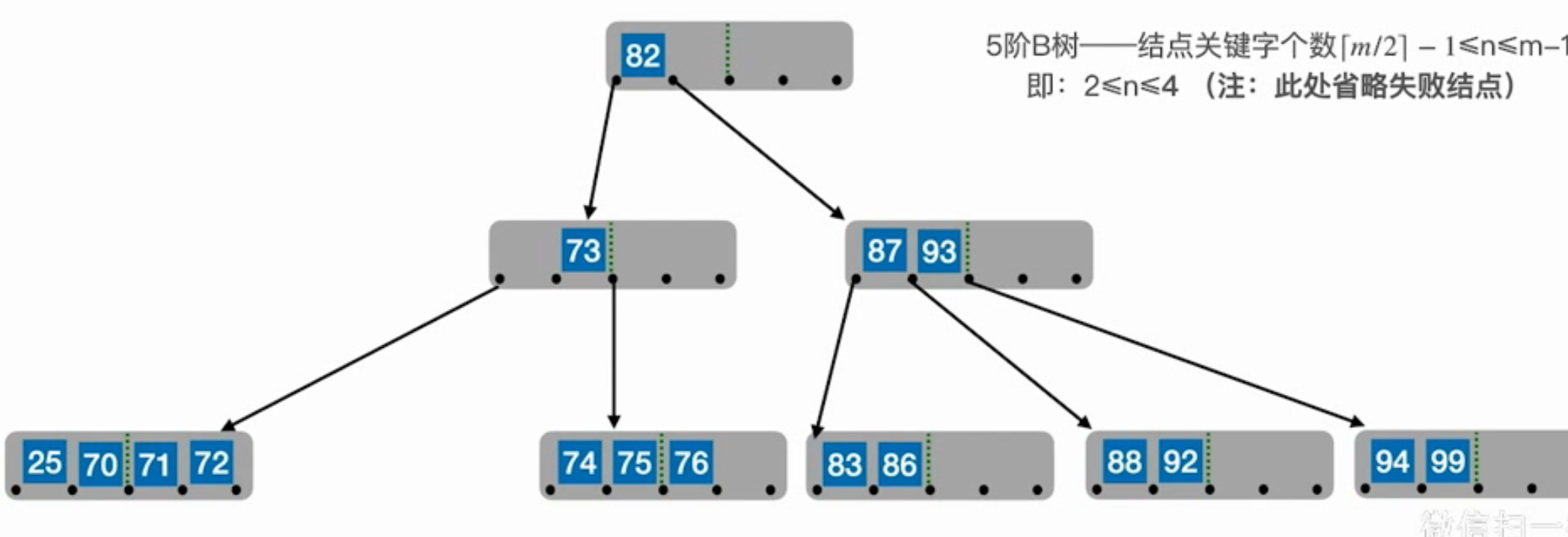

B树总结

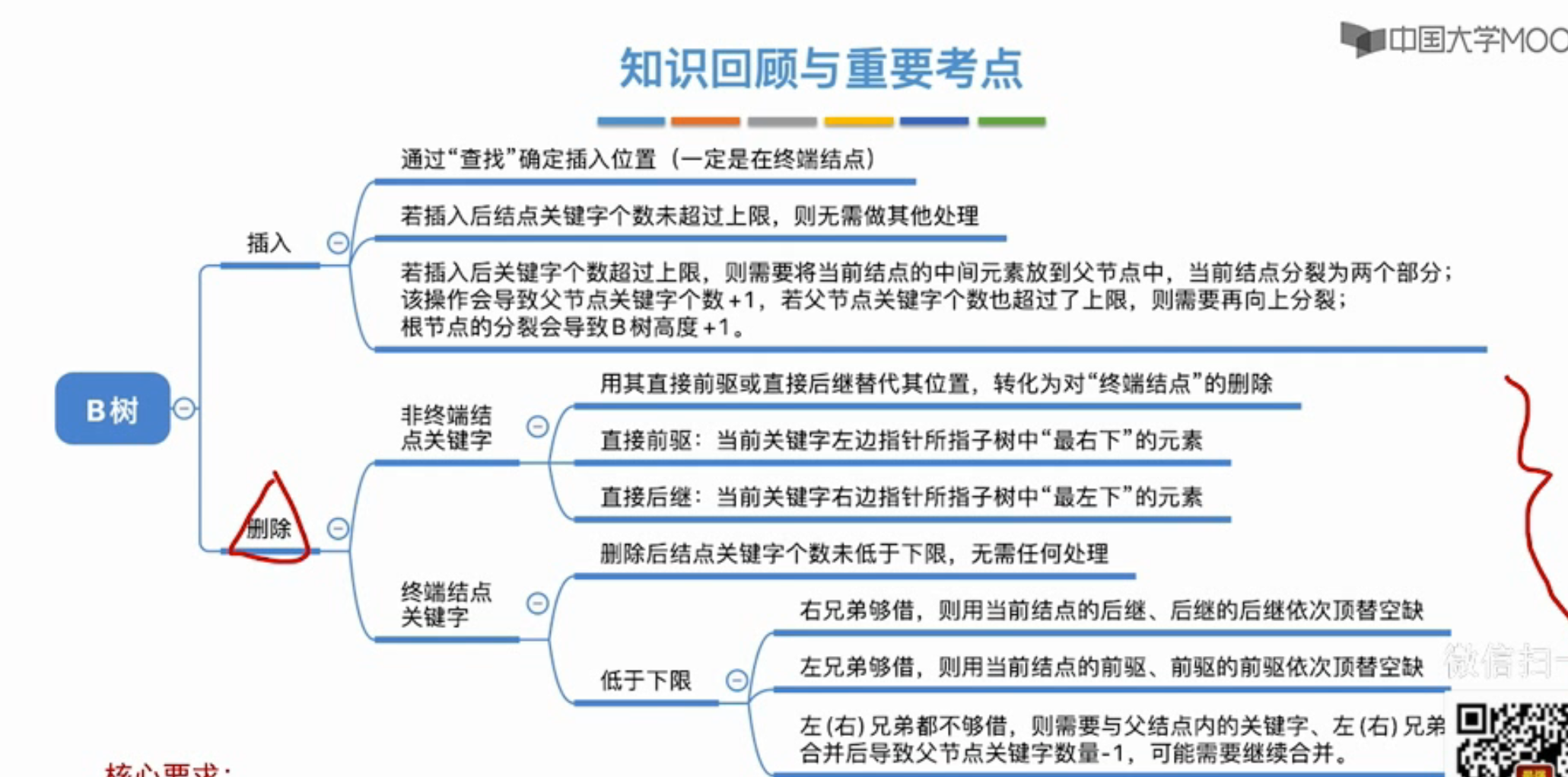
B+树

看一下分块查找

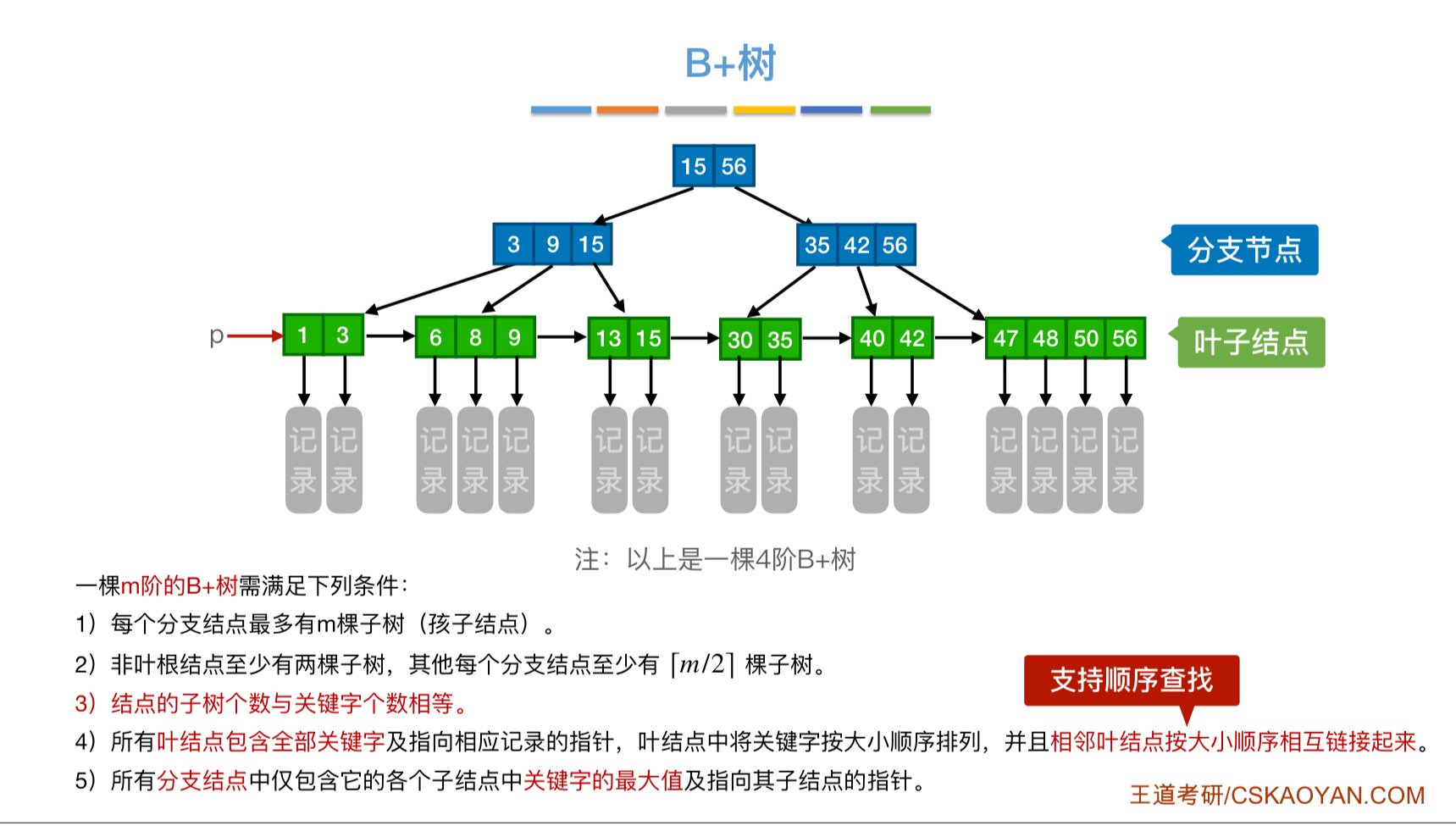
B+树的查找就像分块查找一样必须查找到最后一层，才能获得信息

散列表、哈希表HashTable

定义

一种数据结构
Address=f(key)

冲突的定义：不同的key得到了相同的哈希地址
同义词的定义：具有相同函数值的key对于哈希函数来说是同义词

构造哈希函数

一个好的哈希函数应该能够使对于关键字集合中的任意一个关键字，映射到地址集合中任何一个地址的概率是相等的，称为均匀函数，能够减少冲突

直接定址法

$Hey(key)=a*key+b$

线性变化，关键字集合与地址集合称线性关系，不会有冲突，但很少用
木桶法

除留余数法

很重要，也是最常用的构造函数
取关键字被某个不大于哈希表长m的数p除后取余
$Hey(key)=key\pmod p \qquad p \le m$
p的选取很关键
一般选取p：不大于m但最接近或等于m的质数(如果p小于m，则表中就会一直有空项)
实际运用要按照数字特点去选取

处理冲突的方法

拉链法

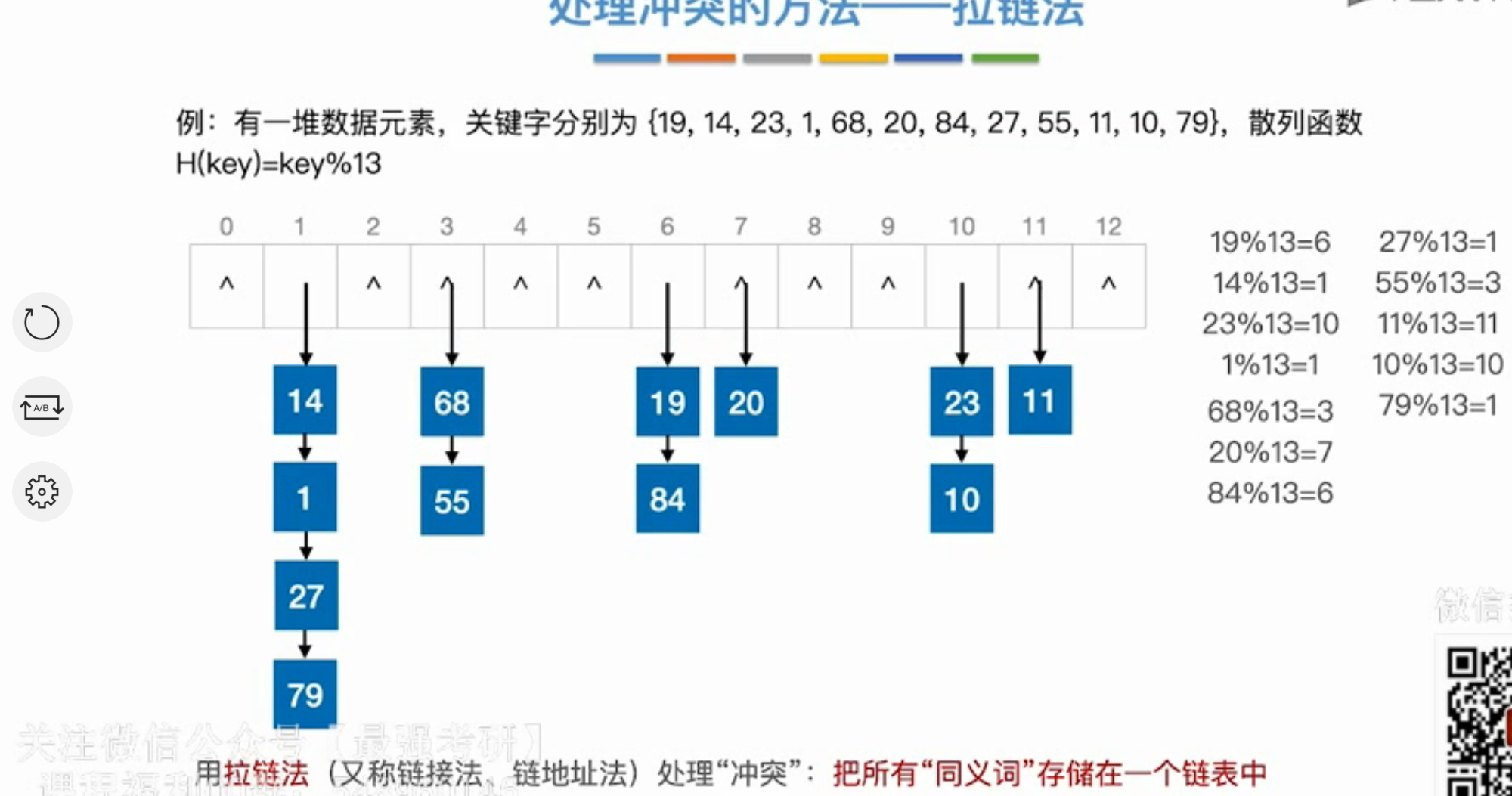
分析ASL

对空指针的判断不算比较(一般)
成功$ASL=\frac{i*位于第i层的同义词个数}{n}$
失败$ASL=\frac{n}{m}$m为表长？？
装填因子$\alpha =\frac{n}{m}$装填因子会直接影响查找效率

开放定址法

可存在新表项的空间既向它的同义词开放，又向它的非同义词开放
$Hi=(H(key)+d_i)\pmod m$
m=表长
i=第几次冲突$i{max} \le m-1$
$d_i$=增量序列
$H_i$=第i次冲突后，key得到的新地址
先解释一下上面的递推式子，假如我们放一个$key$，$H(key)$已经有人了，那么产生第一次冲突，i为1，带入公式产生新地址$H_1$，如果还是有人，i++,继续产生新地址

查找
也按照开放地址来，把按顺序走完$H、Hi$，直到找到或发现为空时停止，注意 _这里的空位置也算做一次比较

由于这个查找特性，使得开放定址法在删除元素时，不能直接删除，而是标记删除，即逻辑删除。

不同的增量序列就称为不同的方法

线性探测法

$d_i=i$，就没发生一次冲突就往后走一个，走到最后一格还能走的话，就从开头走
缺点：造成同义词和非同义词的聚集现象，影响查找效率

平方探测法

${d_i}={1^2,-1^2,2^2,-2^2,\cdots ,k^2,-k^2}\quad k \le m/2$

注意只有m是一个可以表示成$4j+3$的素数时才能使用这个方法

伪随即序列法

再散列法

多准备几个哈希函数，冲突了就用另一个