MH's Blog
0%

最短路径问题

发表于 更新于 分类于

最短路径

BFS算法

解决单源无权图最短路径问题
从修改BFS算法开始

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
void BFS(G,int x)
{
    int distance[G.venum];//去哪要走的路程
    int path[G.venum];//从哪来的
    for(int i = 0; i < G.vexnum; ++i)
    {
        path[i] = -1;
        distance[i] = INT_MAX;
        G.visted[i] = false;
    }
    EnQueue(Q,x);
    int i = x;
    while(!Empty(Q))
    {
        DeQueue(Q,v);
        for (w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w))
        {
            if (G.visited[w])
            {
                continue;
            }
            path[w] = v;
            distance[w] = distance[v] + 1;
            G.visit[w] = true;
            EnQueue(Q, w)
        }
        
    }
}

Dijkstra算法(迪杰斯特拉算法)

可求带权图单源最短路径(也可求各顶点间)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
void DIJ(G,v)
{
    int final[G.vexnum] = {0};//是否已经找到最短路径 1为真
    int dist[G.vexnum];//距离
    int path[G.vexnum];//顶点前驱
    final[v] = 1;
    int INFINITY;
    for(int i = 0; i < G.vexnum; ++i)
    {
        dist[i] = getDist(G,v,i);//获取dist
        path[i] = (getDist(G,v,i) < INFINIY) ? v : -1;
    }
    for(int i = 0; i < G.vexnum; ++i)
    {
        int min = INFINITY;
        int k = v;
        //找dist里没有被确定的与v路径最小的点
        for(int w = 0; w < G.vexnum; ++w)
        {
            if(!final[w])
            {
                if(dist[w] < min)
                {
                    min = dist[w];
                    k = w;
                }
            }
        }
        //已经找到 更新path和dist
        final[k] = 1;
        for(int j = 0; j < G.vexnum; ++j)
        {
            if(!final[j] && (min + getDist(G,v,j)) < dist[j])
            {
                dist[j] = min + getDist(G,v,j);
                path[j] = k;
            }
        }
    }
}

时间复杂度分析

  • 第一个for循环$O(n)=n$
  • 第二个for循环$O(n)=n^2$
    总复杂度$O(n)=n^2$

若求各顶点间的路径长度调用$n$次DIJ即可

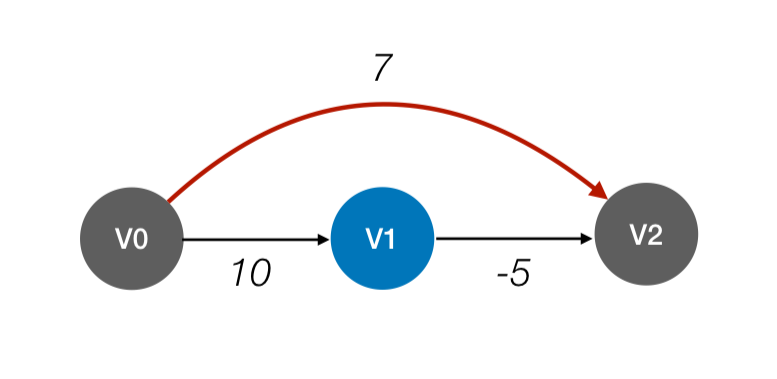
Dijkstra算法缺陷

无法计算负权值带权图
截屏 2021-03-12 下午11.17.54

Floyd算法

动态规划

对于一个G，有n个顶点 要求$vi \rightarrow vj$间的最短路径

  • 直接从$vi \rightarrow vj$的路径为最小路径
  • 允许从$v0$进行中转$vi \rightarrow v0 \rightarrow vj$的路径与最小路径相比
  • 一直重复$vi \rightarrow v0 \rightarrow … \rightarrow v(j-1) \rightarrow vj$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void FLOYD()
{
    for(int k = 0; k < n; ++k)//允许从第k个点进行中转
    {
        for(int i = 0; i < n; ++i)
        {
            for(int j = 0; j < n; ++j)
            {
                if(A[i][j] > A[i][k] + A[k][j])
                {
                    A[i][j] = A[i][k] + A[k][j];
                    path[i][j] = k;
                }
            }
        }
    }
}

缺陷：无法求解负权回路(因为越走就越小)