MH's Blog
0%

图的存储

发表于 更新于 分类于 
graph TD;
A(图的存储);;
A-->B1(邻接矩阵)==>C1[数组实现,空间复杂度高];
A-->B2(邻接表)==>C2[顺序存储+链表实现];
A-->B3(十字链表)==>C3[存储有向图];
A-->B4(邻接多重表)==>C4[存储无向图];
C3-->D1(代码复杂考研很少考);
C4-->D1;

邻接矩阵法

1
2
3
4
5
6
7
8
9
10
11
#define VertexType int
#define MAXVertexNum 100
#define INFINITY 100//如果边的权值大于等于该值，称该边无穷长
struct MGraph
{
    VertexType Vex[MAXVertexNum];//顶点
    int Edge[MAXVertexNum][MAXVertexNum];//邻接矩阵
    int vexnum;//当期顶点树
    int arcnum;//当前边数/弧数
};

对于无向图来说：邻接矩阵具有对称性

无向图的第i个顶点的度：第i行或第i列的非零元素个数($E\neq0$的个数)
有向图的第i个顶点的度： 出度：第i行非零元素个数 入度：第i列的非零元素个数 度=出+入

性能分析：空间复杂度$O(n)$ 只适用于存储稠密图
对于无向图可采用对称矩阵的压缩压缩存储

策略：存储主对角线和下三角区，按行优先
$a_{i, j}\rightarrow B[k]$
$k=\frac{i(i-1)}{2}+j-1 $

一些性质：
图G的邻接矩阵为A(矩阵元素为0/1, 即不带权值)，则$A^n$中的$a^n_{i, j}$就为由$i$到$j$的长度为$n$的路径数目

邻接表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

#define VertexType int
#define MAXVertexNum 100

typedef struct ArcNode
{
    int adjvex; //边指向哪一个顶点(下一个) 即AdjList[adjvex]
    ArcNode *next;
    int info;//权值
}ArcList;

typedef struct VNode
{
    VertexType data;
    ArcList first;//第一条边(随便指一条)
}AdjList[MAXVertexNum];

struct ALGraph
{
    AdjList vertices;//邻接表
    int vernum;
    int arcnum;
};

性能分析：
对无向图：每条边有两个顶点，所以空间复杂度为$O(2|E|+|V|)$
对有向图：空间复杂度$O(|E|+|V|)$

计算度：
对无向图：遍历对应的链表
对有向图：

  • 出度：遍历对应链表
  • 入度：遍历除自己外所有对应链表

十字链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
typedef struct AcrossAcrNode
{
    int tailvex;//弧尾点编号
    int headvex;//弧头点编号
    int info;
    AcrossAcrNode *hlink;//弧尾相同的下一条弧
    AcrossAcrNode *tlink;//弧头相同的下一条弧
};

typedef struct AcrossVNode
{
    VertexType data;
    AcrossAcrNode *firstin;//以该节点为弧头的第一条弧
    AcrossAcrNode *firstout;//以该节点为弧尾的第一条弧
}AVList[MAXVertexNum];

struct AcrossGraph
{
    AVList vertices;//十字链表
    int vernum;
    int arcnum;
};

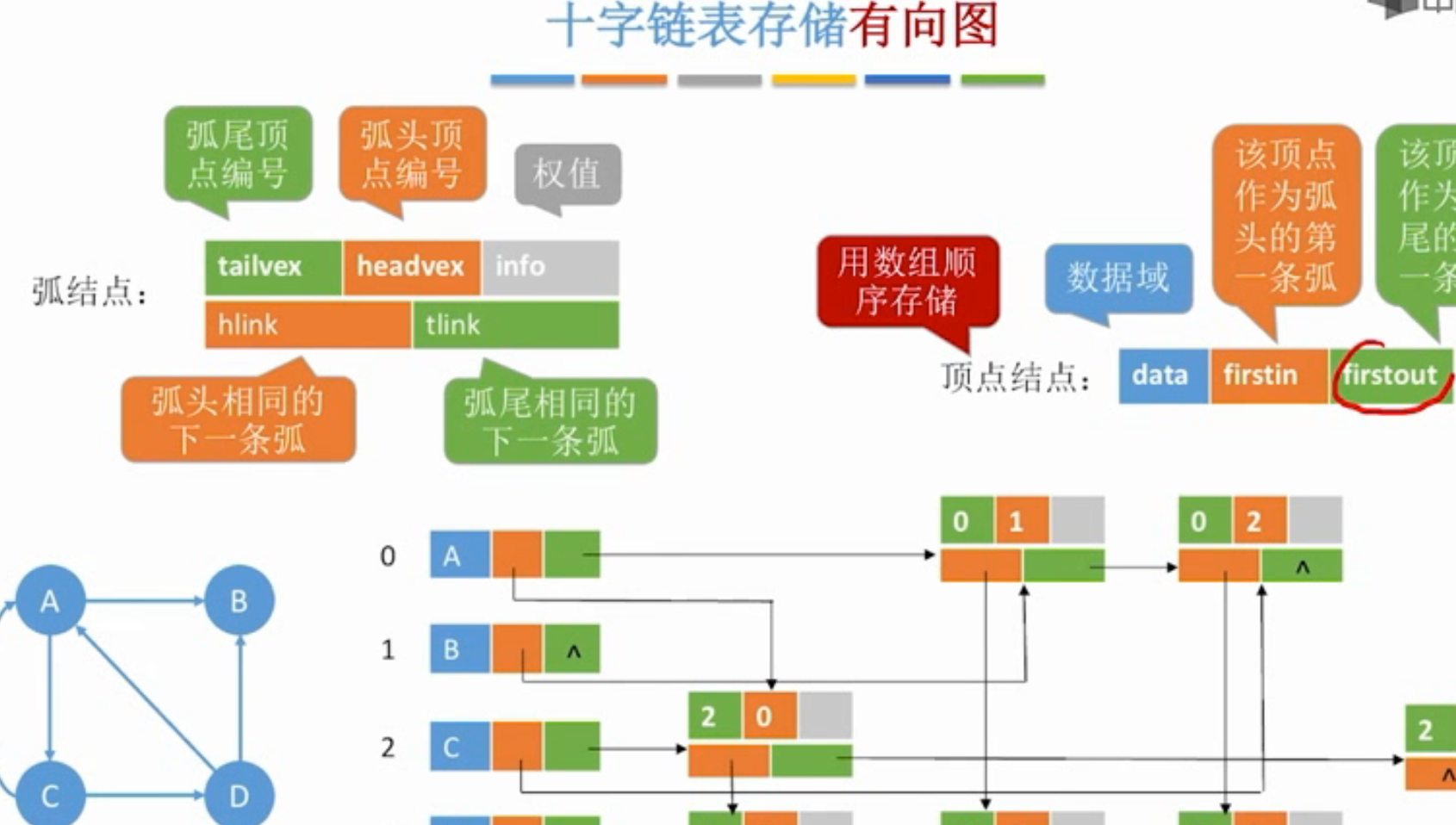
Screenshot 2020-11-25 at 10.55.27 PM

性能分析：
空间复杂度$O(\lvert E \rvert +\lvert V \rvert)$
找到入边：顺着hlink一直找
找到出边：顺着tlink一直找

邻接多重表

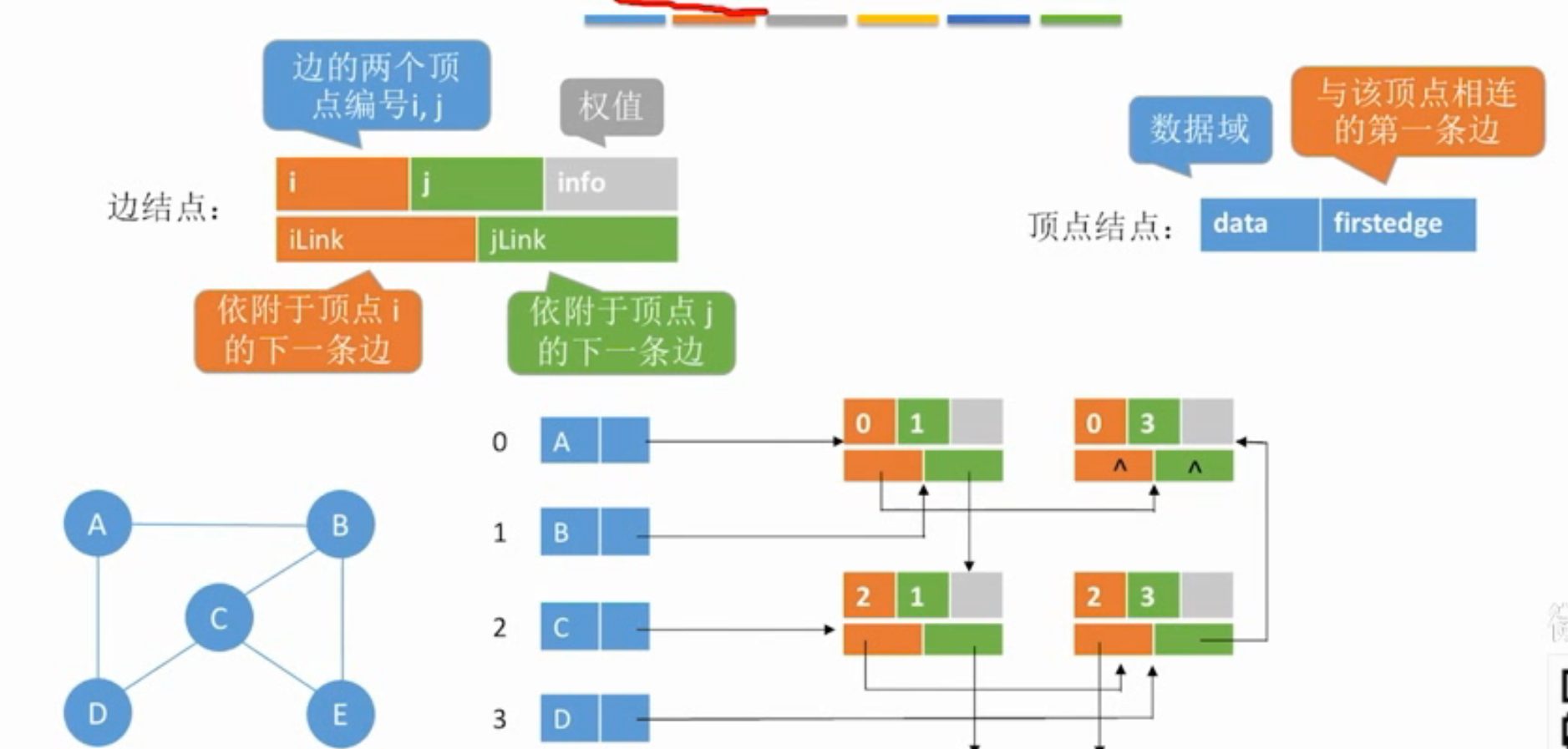
Screenshot 2020-11-25 at 11.01.40 PM

总结

邻接表 邻接矩阵 十字链表 邻接多重表
空间复杂度 无向图$O(2\lvert E \rvert + \lvert V\rvert )$ 有向图$O(\lvert E \rvert +\lvert V \rvert )$ $O(\lvert V^2\rvert)$ $O(\lvert E \rvert +\lvert V \rvert )$
适合于 储存稀疏图 储存稠密图 有向图 无向图
表示方式 不唯一 唯一 不唯一 不唯一
计算度 计算有向图的度、入度不方便 遍历对应行 老方便了 老方便了
找相邻边 找有向图的入边不方便 遍历对应行 老方便了 老方便了
删除边或顶点 删除边很方便，删除点要移动大量数据 无向图不方便 老方便了 老方便了